"Ползунок"

Эта игра была придумана Д. Силверменом, автором довольно известной книги "Ваш ход". Игровое поле (рис. 5) представляет собой решетку размером 5×6 точек (можно играть и на полях других размеров).

Рис. 5

Играют двое, проводя по очереди горизонтальные или вертикальные "единичные" отрезки. Требуется, чтобы получающаяся траектория игры была непрерывной, однако присоединять новый отрезок к уже имеющейся ломаной можно с любого конца. Проигрывает тот, кто вынужден своим ходом замкнуть траекторию. Например, в позиции на рис. 6 тот, чья очередь ходить, проигрывает.

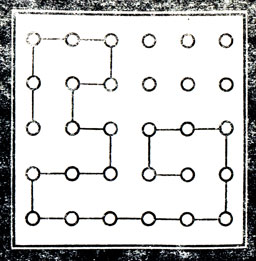
Рис. 6

Для поля размером 5×6 задача поиска оптимальной стратегии очень проста. Ясно, что первый игрок может выиграть, начиная ходом с центрального ребра, а затем делая ходы, симметрично противоположные предыдущему ходу противника. Но этот способ не годится при многих других размерах поля. Общую оптимальную стратегию первым предложил Дж. Миллер. Она состоит в следующем.

Выигрышная стратегия

Предположим сначала, что число точек решетки четное. Вычертим по ребрам решетки такую линию, которая проходит через каждую точку решетки ровно один раз (так называемый гамильтонов путь), и покрасим ребра, входящие в нее, через одно в красный цвет, начиная и кончая красным (это возможно, поскольку число точек четное). Используя этот рисунок, первый игрок может обеспечить себе победу, всегда играя по красным ребрам.

Пример партии, где первый игрок побеждает этим способом, показан на рис. 7, б; на рис. 7, а изображен вспомогательный гамильтонов путь, красные звенья которого показаны пунктиром. Рядом с каждым ходом указан его номер.

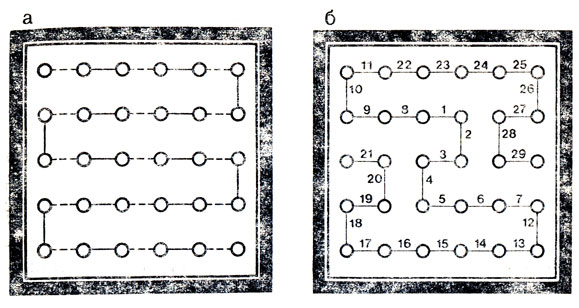
Рис. 7, а, б

Если число точек решетки нечетное, побеждает второй игрок. Ему следует провести (конечно, мысленно!) гамильтонов путь, начиная с любой из двух точек, соединенных первым ходом противника, покрасить его, как в случае, который был рассмотрен, а затем всегда играть по красным ребрам. Пример партии с применением этой стратегии продемонстрирован на рис. 8, который составлен аналогично рис. 7.

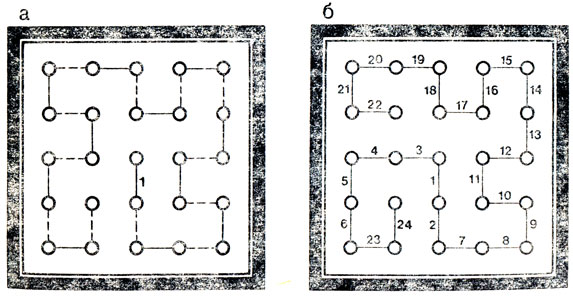
Рис. 8