III. На границе математики и развлечения: Шахматная доска и геометрическая прогрессия. Задачи для коня. Проблема Эйлера. Магические квадраты. Ходом коня. Задачи для ферзя и ладьи. Число комбинаций расстановок фигур. Число вариантов игры. Попытки создать математическую теорию шахматной игры. Доказательство категоричности шахмат. "Ничья" или победа определенной стороны? Смерть теории "ничьей"

'Подождите, пожалуйста, мы должны закончить партию...' ('Цейт им Бильд')

На необитаемом острове. (Рис. К. Баранецкого в 'Карусели')

Согласились на ничью. (Рис. И. Зубова - 'Огонёк')

'Шах королю!' (Рис. Е. Косерадзского - 'Шпильки')

'Мы не знаем, какую купить игру'? (Рис. И. Гегена - 'Фришер Винд')

Нервозность. (Рис. А. Франсуа)

'Это некрасиво! Все на одного...' (Рис.К. Кламанна - 'Уленшпигель')

Сколько раз говорят о рождении шахмат, столько по традиции приводят рассказ о шахматной доске и зернах хлеба. Известен он вам? Если нет, послушайте.

Это было давным-давно, тысячи полторы лет назад. Индийский властелин Схерам (или Схехрам) не отличался ни слишком большим организационным талантом, ни умением управлять, а потому в короткое время довел государство до разорения. Тогда один брамин мудрец Сесса, сын Дагера, желая тактично сделать замечание суровому королю по поводу его неправильного поведения, придумал игру, в которой король - самая важная фигура - не может ничего достичь без помощи других фигур и пешек. Шахматы были показаны властелину, и шахматная игра якобы произвела на него сильное впечатление. Желая отблагодарить Сессу за наглядный урок жизненной мудрости и за интересную игру, Схерам обещал наградить его всем, что он только пожелает. Сесса, воспользовавшись случаем дать чванливому королю еще один урок, на сей раз урок скромности, потребовал, казалось бы, небольшого вознаграждения. Он попросил выдать ему со склада такое количество пшеницы: на первую клетку шахматной доски положить одно зерно, на вторую - 2 зернышка, на третью - 2 X 2, т.е. 4 зернышка, на четвертую - 4x2, т.е. 8 зернышек, и так далее в порядке геометрической прогрессии - на все 64 клетки шахматной доски. Властелин согласился, радуясь, что так легко отделался. Но когда из амбаров начали поставлять зерно, то очень скоро выяснилось, что желание мудреца выполнить невозможно. Ибо пословица "Зернышко к зернышку - будет мешок" обрела на этот раз вполне конкретную форму.

Когда потом все было подсчитано, получилось, что на 64-ю клетку пришлось 87 076 425 546 692 656 зерен, а общее количество причитающегося зерна, составляющее сумму чисел, возведенных в степень от 0 до 63 (1 +21 +22 + +23+24 и т.д.) составляет 18 446 744 073 709 551 615 зерен (это значит 18 квинтиллионов 446 квадриллионов 744 триллиона 73 биллиона 709 миллионов 551 тысяча). В перечислении на емкость это составляет: 922 337 203 685 кубических метров пшеницы, считая, что на один кубический метр приходится 20 миллионов зерен (на 1 см3 - 20 зерен).^*

^* (Перельман в книге "Живая математика" в главе, посвященной "Легенде о шахматной доске", дает иной подсчет объема зерна: один кубический метр пшеницы содержит около 15 миллионов зерен; требуемое брамином количество пшеницы составило бы - 12 000 000 000 000 куб. метров. Если бы построить амбар для этого количества зерна: 4 метра высоты и 10 метров ширины - его длина составила бы 300 000 000 километров, т.е. в два раза больше, чем расстояние от Земли до Солнца.)

Для получения такого количества зерна следовало бы восемь раз засеять поверхность земного шара и столько же раз собрать урожай.

Эти вычисления, по правде говоря, не имеют непосредственной связи с сущностью шахмат, но, так сказать, символически показывают неожиданные математические результаты, скрывающиеся за пределами черно-белой шахматной доски. Однако, если мы хотим быть математически точными, следует отметить, что рассказ о молниеносно умножающемся количестве зерен возник не в Индии, вообще-то колыбели шахмат, а в стране, отличающейся скорее традициями гуманитарно-философских наук. Рассказ сложили арабы - мастера точных наук.

В арабской рукописи сохранились следы пользования шахматной доской как своего рода вспомогательными счетами для калькуляции.

Связь финансовых расчетов с шахматной доской была увековечена в Англии, где от названия шахматной доски (по-французски l'echiquier) происходит слово "эксчекер" (exchequer), что означает главное финансовое управление, государственная казна. Прежде распределение государственного бюджета производилось на специальной шахматной доске, где каждая клетка обозначала определенный вид расходов. Путем передвижения денежных сумм с одной клетки на другую окончательно определялись платежные статьи бюджета. В истории известен и такой случай, когда решение о распределении финансового дохода принималось в зависимости от результата разыгранной шахматной партии. Это не имеет, конечно, ничего общего с цифровыми свойствами шахматной доски, а скорее может служить примером очень упрощенного способа решения сложных расчетов, связанных с имуществом. В свое время в Ирландии жили два рода, представители которых разыгрывали партию шахмат в присутствии служащего, ведущего официальный протокол. Выигрывавшая сторона имела право в течение года получать доходы с имения противника.

Брамин, султан и шахматы - в интерпретации художника Г. Миклашевского...

...и та же тема возникновения шахматной игры в трактовке другого польского художника М. Покоры

Однако, приведенный анекдот отвлек наше внимание от основных рассуждений, которыми мы должны заняться, т.е. от математических исследований. Прежде всего, следует особо подчеркнуть, что большинство математических научных трудов и исследований о шахматах связано не с теорией самой игры, а с решением цифровых тайн шахматной доски и движений по ней разных фигур. Усилия создать математическую теорию шахматной игры не приносят до сих пор результатов, хотя бы таких очевидных, как, например, применение геометрии в рассуждениях о биллиарде. Пожалуй, самой большой среди известных работ является научный труд в трех томах русского профессора математики, шахматного теоретика К. Яниша (1862 г.), написанный на французском языке и посвященный применению математического анализа в шахматной игре. Автор исследует количество комбинаций и расстановку фигур на шахматной доске, определяет силы фигур в отдельных позициях, ценность обмена и т.д. Современный труд в этой области пера бельгийского специалиста М. Крайчика не выходит за пределы тех же рамок. Автор особенно тщательно обработал интересные цифровые данные - проблемы расстановки ферзей на шахматной доске и задачи для коня.

Вопрос о поисках общего метода, разрешающего делать такой ход конем, чтобы он мог пройти все клетки, не становясь два раза на одну и ту же клетку, увлекал математиков в течение двух столетий. Первым подробно исследовал и описал свойства движения шахматного коня великий швейцарский математик Эйлер, издавший во второй половине прошлого столетия труд, анализирующий ход коня в так называемых замкнутых циклах, когда после последнего хода можно возвратиться к исходной точке, закрывая линию, обозначающую ход шахматной фигуры. С того времени эти своеобразные задания для коня в шахматах называются проблемами Эйлера.

Арабская шахматная доска для счета: горизонтальные ряды белых или черных клеток систематизируют числа в арифметической прогрессии, по диагонали - в геометрической

Существуют различные, разработанные несколькими математиками правила передвижения коня по всей шахматной доске с условием (хотя и необязательным) закрытия цикла. Польский автор Ш. Еленьски в популярной книге "Лилявати", посвященной математическим развлечениям, упоминает о четырех методах: Эйлера, Моона (рамочный метод, 1843 г.), Муавра - начала XVIII в. (также рамочный метод, т.е. состоящий в том, что внутри доски выделяется центральный квадрат и "рама" для вспомогательных целей) и, наконец, Рожэ (середина XIX в.) - метод деления шахматной доски на четверти.

Диаграммы, иллюстрирующие ход коня на шахматной доске, образуют часто оригинальные узоры и рисунки, напоминающие сложные геометрические фигуры, числа, буквы, арабески и т. д.

Возможности разных решений задач для коня являются значительно большими, чем это кажется. Число вариантов хода коня (если передвижение ведется на доске с 64 клетками) превышает тридцать один миллион.

Шахматный конь и его родственники. (Рис. Л. Минтыч - 'Пшекруй')

Известны также задачи такого же типа для других фигур, чаще всего для ладьи, а также комбинированные задачи, соединяющие ход коня с движением слона, ладьи или короля. Комбинированные и простые задачи решались с большой страстью еще в Индии, Персии, Аравии и в других странах Востока, о чем сохранились многочисленные следы в рукописях тысячелетней давности и более поздних.

Особого внимания заслуживают решения, в которых не только выполнено условие замкнутого круга, но, кроме того, цифры, определяющие очередные позиции фигур, например коня, составляют "магические" квадраты.

Коль скоро зашла речь о "магических" квадратах, стоит привести один пример, помещенный Ю. Тувимом в сборнике литературных курьезов под заглавием "Пегас дыбом". Это известный средневековый буквенный квадрат, состоящий из пяти загадочных кабалистических слов, в котором ход конем давал добавочное (кроме значения самих слов) решение "мистического" характера (при этом следовало сделать несколько ходов другой фигурой с помощью невыясненного до сих пор ключа).

 С А Т О Р
 А Р Е П О
 Т Е Н Е Т
 О П Е Р А
 Р О Т А С 

Делая ход конем по буквам, мы два раза читаем: ПАТЕР НОСТЕР АО, где буквы А и О обозначают названия греческих букв альфа и омега; в переносном значении это обозначает начало и конец.

Ход шахматного коня, столь оригинальный, характерный и специфический, является ключом для многих ребусов и шарад. Можно ведь приказать коню прыгать по определенной части доски, например вдоль ее краев, или по произвольно выдуманным геометрическим фигурам, составленным, конечно, из многих смежных малых полей. Чаще всего эти задачи заключаются в прочтении с помощью движения шахматного коня какой-нибудь сентенции, составленной из букв, либо слогов, помещающихся в отдельных клетках. Иногда буквы заменяются картинками.

О необычайной идее использования задачи с конем рассказывает советский фильм "Голубые дороги". Действие картины происходит после второй мировой войны. В ней показан героический труд моряков советского военного флота, которые разряжают заложенные гитлеровцами минные поля. Три минных поля, находящихся на коммуникационном пути, приносят особенно много хлопот. Из 36 тяжелых магнитно-звуковых мин, заложенных в каждом поле, минеры разрядили 32 мины. Остальные четыре мины, угрожающие взрывом каждому проплывающему над ними кораблю, обнаружить не удается. Таинственные мины с часовым заводом сосредоточили на себе все внимание отважных моряков. Капитан Ратанов решает любой ценой раскрыть схему расположения ненайденных мин. Анализируя обстоятельства, связанные с конструкцией этих грозных мин, он узнает, что их изобретателем был немецкий инженер, о котором известно также, что он увлекался шахматами, особенно решением задач. Капитан Ратанов был тоже любителем шахмат. Задумавшись над расположением минного поля и вспомнив по ассоциации недавно решенные задачи для коня, он приходит к неожиданному выводу, что мины расположены в шахматном порядке по схеме, ключом к которой является двойной ход конем из центра. Предположение подтвердилось, и мины удалось обезвредить.

Вот как пригодилось знание шахматных правил и любовь к решению шахматных задач! Разгадать тайны минного поля при помощи ходов шахматного коня наверняка не смог бы герой следующего анекдота.

Ласкер во время выступлений в Англии случайно сыграл в шахматы с неизвестным, который, получив очень скоро мат, попросил мастера оценить его игру.

- У вас какой-то странный способ игры, - ответил Ласкер. - Почему, например, вы ни разу не пользовались конем?

- Почему? Да ведь я не имею ни малейшего понятия, как двигать конем...

Но мы опять уклонились от темы.

Многих ученых, размышлявших о шахматах, увлекала не только проблема продвижения разных фигур по шахматной доске, но и возможность расстановки нескольких фигур так, чтобы они выполняли определенные условия. Например, чтобы они блокировали самое большое количество клеток, чтобы не били взаимно друг друга и т.д.

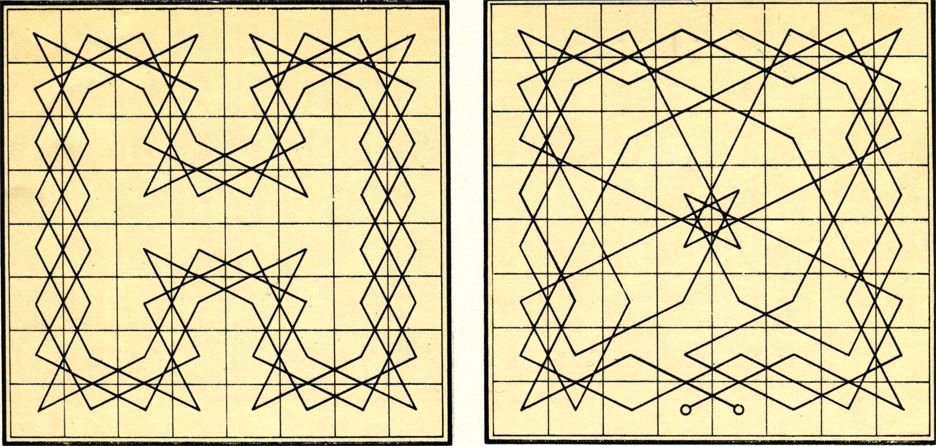
Диаграммы задач для коня, показывающие такой проход коня по всему шахматному полю, при котором он ни разу не становился на одну и ту же клетку дважды

Можно, например, поставить на шахматной доске пять ферзей так, что они будут блокировать все квадраты 4860 способами.

Большую известность получила задача с восемью ферзями, которые не могли взаимно бить друг друга. Немецкий математик Гаусс первым подсчитал, что имеются 92 позиции, исчерпывающие все возможные комбинации в этой области. Основных расстановок имеется только двенадцать, остальные мы получаем путем поворотов шахматной доски или с помощью симметричных расстановок (как бы отраженных в зеркале).

Такая же задача, но с участием 8 ладей, имеет не менее 40 320 разных позиционных расстановок. Еще большее число комбинаций возникает при расстановке 8 слонов или коней. До сих пор еще не удалось точно установить это число: просто никто не потрудился над тем, чтобы довести счет до конца.

Но зато много бумаги и времени ушло на вычисление количества комбинаций при расстановке принимающих участие в игре фигур; это уже имеет некоторое вспомогательное значение для теории игры, а не является лишь развлечением, как при задачах для коня и ферзя.

Было подсчитано, что два короля можно поставить в 3612 позициях. Ввод на шахматную доску одной только пешки увеличивает эту цифру до 167 248 правильных позиций (здесь, например, не учитывается положение, когда белая пешка находится на первой линии и т.д.). Два короля и две пешки можно поставить примерно в 7 400 000 позициях. Внимание! Мы опять начинаем оперировать миллионами! Посчитаем дальше: два короля и две фигуры дают свыше 13 миллионов комбинаций. И, наконец, количество позиций, в которые можно поставить два короля, двенадцать фигур и одну пешку, заканчивается 27-значным числом.

Решение древней арабской задачи: фигура движется по всем клеткам шахматного поля то как конь, то как слон. Слон движется прыжками через одну клетку

Задача на движение по полю попеременно ходом ферзя и коня. Ферзь ходит только на расстояние одной клетки во всех направлениях - согласно прежним условиям

Мы приближаемся к кульминационной точке жонглирования цифрами, а именно: 32 шахматные фигуры можно поставить на шахматной доске с 64 клетками в количестве комбинаций, составляющем 7 534 686 312 361 225 327 х 10³³.

В этом головокружительном числе количество действительно возможных расстановок представляет только незначительную часть.

О том, как с каждым новым движением, начиная с исходной позиции, возрастает количество вариантов игры, убеждает хотя бы следующий перечень:

Белые могут сделать первый ход 20 разными способами (16 ходов пешками и 4 конями). Черные в ответ имеют такие же возможности.

Второй ход белые могут выбрать среди 28 возможных, а черные в своем распоряжении имеют 29 ответов.

В третьем ходе белые имеют для выбора 30 комбинаций, черные - 31, в четвертом белые - 32, черные - 33 комбинации.

При первом же ходе обеих играющих сторон уже имеется 400 (20x20) разных вариантов игры. Для упрощения дальнейших подсчетов предположим, что первые пять ходов обеих сторон имеют по 20 возможностей, а следующие - по 30 возможностей выбора хода. Кроме того, можно считать, произвольно конечно, что в среднем партия имеет около 40 ходов.

Итак, мы можем подсчитать, сколько разновидностей шахматных партий имеется в распоряжении игроков. Это, конечно, неправильный подсчет, ибо некоторые партии могут закончиться и при меньшем количестве ходов, а другие, наоборот, могут продолжаться дольше, но все дело в том, чтобы составить приблизительное понятие о количестве возможных комбинаций. А счет выглядит так: (20 х 20)⁵ х (30 х 30)³⁵ = 2¹⁰ х 3⁷⁰ х 10⁸⁰ = 25 х 10¹¹⁵

Распространенный вид умственного развлечения: буквенная задача для коня. Начиная с буквы 'R', надо пробежать конем по всем клеткам, постепенно решая задачу. Подобные задачи можно часто встретить на страницах печати

В результате мы получаем число из 117 цифр, т.е. во много раз большее, чем количество разных расстановок всех 32 фигур, что и понятно: увеличивается число позиций с переменным количеством пешек и фигур вследствие их выбывания из игры.

Кто-нибудь может упрекнуть нас в том, что полученное число слишком преувеличено, так как содержит много вариантов, которые уже после первых нескольких ходов можно было бы устранить как бессмысленные. Стало быть, мы должны сделать еще один подсчет с более простыми ограничениями, но лучше объясняющий бурный рост количества действительных вариантов партии уже после нескольких ходов.

Тип геометрической задачи для коня: на одной из свободных клеток шахматного поля надо так поставить коня, чтобы затем, при помощи минимального количества ходов, взять все черные пешки. (Б. Кордемский 'Математическая смекалка'.)

Если, например, при определенном варианте начала игры есть основание думать, что при трех или четырех точно определенных ходах обеих сторон мы имеем по два хороших хода для выбора, то уже после семи ходов мы имеем свыше 16 тысяч рациональных расстановок. А если в начальном этапе игры было бы три хороших хода, то после семи ходов количество комбинаций составило бы почти 5 миллионов. И все это в одном только варианте начала.

Я думаю, достаточно арифметики. Ведь совершенно ясно, что практически мы имеем в игре неограниченное количество комбинаций. А значит, в течение еще многих сотен тысяч лет угроза того, что в шахматах будут исчерпаны все варианты игры, не страшна человечеству.

Математика до некоторой степени может помочь упрочению теоретических рассуждений об игре, но не может создать этой теории. Математическая шахматная теория не существует и не может быть создана. Об этом, в частности, пишет известный французский математик Г. Пуанкарэ, рассуждая о построении научных гипотез. По его мнению, движения на шахматной доске могут быть каждый раз другие как в одной партии, так и во многих других и не составляют какого-то ряда, имеющего математическое обоснование. На основании выполняемых ходов невозможно выработать никаких обобщающих тезисов, следовательно, не может быть и речи о науке. Шахматист предусматривает несколько ходов вперед, не имея возможности на практике проанализировать слишком большое количество ходов (ведь число комбинаций растет в зависимости от развития игры), он руководствуется скорее чутьем и избранной тактикой, не опираясь на точно проверенном подсчете возможностей.

Если бы мы могли проанализировать все варианты (до самого конца партии), которые могли бы возникнуть в определенный момент игры, то пришли бы к уточнению некоторых правил игры. Однако только правил, а не научной теории. И действительно, во многих эндшпилях мы сумеем получить ответ на вопрос, как играть, чтобы довести партию до победы, или же какой будет результат в зависимости от выбора хода. Это не оправдывается в дебютах. Может случиться, что в дебюте, который считается правильным, существует незамеченный до сих пор ход, опровергающий ценность варианта. Отсюда вывод: ни один дебют не имеет математического доказательства абсолютной правильности.

Если же не обращать внимания на практическую сторону игры, когда мы, собственно говоря, имеем дело с неограниченными возможностями для выбора и ведения игры, в связи с чем невозможно выработать математическую теорию, то с точки зрения чисто научного рассуждения шахматную игру можно подчинить очень простым принципам. Но не надо обольщаться преждевременно. Несмотря на то, что сущность шахмат полностью определена, это ни в малейшей степени не влияет на самую игру. Хотя это и звучит парадоксально, но такова действительность.

Стало быть, шахматы имеют огромное, но не бесконечное количество комбинаций, а правила игры вносят дополнительные ограничения: после троекратного повторения одной и той же позиции наступает ничья, так что при большом количестве ходов можно почти механически довести игру до ничьей, если одна из сторон не победила раньше. Значит, растянуть игру до бесконечности невозможно. Это могло бы наступить, если бы не обязывали правила ничьей. Тогда, например, так называемый "вечный шах" был бы действительно вечным шахом, а не ничьей.

Больше того, можно обстоятельно и точно доказать, что шахматы являются игрой с заранее предрешенным результатом. На сегодняшний день мы еще не можем сказать, каким именно результатом окончится партия, то есть всегда ли выигрывают белые или черные или же результатом каждой правильно разыгранной обеими сторонами партии является ничья.

Интересно пишет об этом Г. Крохмальны в статье об играх, напечатанной несколько лет назад в польском журнале "Пшекруй".

"Никто не сомневается, что шахматы основаны на умозаключениях. Это поочередная игра: противники делают ходы попеременно. Начальная позиция всегда одна и та же, и всегда начинают белые. Шашки, "волк и овцы" и многие другие игры (даже детская "виселица") принадлежат к тому же типу...

Если бы нашлось сто демонов, одаренных умением обдумывать шахматные комбинации, произвольно длинные и произвольно обширные, и они бы участвовали в шахматном турнире, то на всех пятидесяти досках выиграл бы один и тот же цвет..."

Без подписи. (Рис. Е. Флисака - 'Шпильки')

Бельгийский аптекарь Г. Д. Хооге рядом с сконструированной им электрической машиной для решения задач для коня. После того, как машине дана соответствующая задача, она автоматически начинает ее решать, поочередно освещая на большом шахматном поле клетки, на которые якобы ступает конь. Машина демонстрировалась на XIV шахматной Олимпиаде в Лейпциге в 1960 году

Внизу: вид сложной конструкции аппарата с сетью тысяч электрических проводов

Итак, из этого следует, что в случае идеальной, т.е. безошибочной игры, результат ее предрешается для одной стороны; это значит, что не может быть и речи о справедливой исходной расстановке. Один игрок пользуется привилегиями, так же как в игре "волк и овцы" всегда выигрывает тот, кто руководит движением "овец".

Не опираясь на слишком тщательные теоретико-логические исследования, а наблюдая за розыгрышем многих партий и делая выводы из собственного опыта, многие шахматисты пробовали решить, к чему на практике ведет шахматная игра, если играют два мастера, хорошо знающие все дебюты. "Хорошо" означает - в пределах человеческих возможностей.

Знаменитый французский шахматист Филидор считал, например, что тот, кто начинает игру и не делает ошибок, должен выиграть. А Ласкер и большинство современных ему мастеров склонялись к тому, что по мере развития науки о шахматной игре партии должны оканчиваться вничью. Нашлись и такие "эксперты", а было это в десятые и двадцатые годы нашего века, которые утверждали, что шахматная игра перестает интересовать человечество и постепенно умирает. Умение играть якобы является настолько достаточным, что предопределяет ничейный результат, если ни одна из сторон "не отклонится" и не сделает непредвиденного хода в якобы упорядоченном знании о дебютах шахматных партий.

Однако не все поддались чарам "теории ничьей". О большом чувстве юмора противников этой точки зрения свидетельствует бывший в то время в ходу анекдот в форме восточной сказки.

Во времена царствования султана Гаруна-аль-Рашида в Багдаде процветала игра в шахматы. Играли буквально все: старые и молодые, мужчины и женщины, бедные и богатые. Однажды в городе появился мудрец, который объявил, что он может указать способ, как после каждого очередного хода найти самый лучший ответный ход. Это возбудило огромный интерес среди населения. В конце концов мудрец открыл свой способ. И что же оказалось? Им стали пользоваться оба партнера. Игра стала неинтересной, результат не давал решения. Всем расхотелось садиться за шахматную доску. Люди загрустили, исчезли оживленные группы болельщиков. В повседневной жизни не стало приятного, так занимающего всех развлечения. Спасая положение, рассудительный халиф приказал конфисковать труд мудреца, а учителей в школах обязал не обучать никого такому "совершенному методу".

Ирония этого поучительного рассказа бьет в самую суть вопроса. Действительно ли спасение заключалось в отказе от всякого знания о шахматной игре и в доведении розыгрыша до сражения, ведущегося случайно и вслепую? Жизнь сама дала лучший ответ на этот вопрос.

В ничейную смерть шахмат поверил даже чемпион мира гениальный кубинец Капабланка. Он и его почитатели считали, что человек уже постиг максимум вариантов отдельных партий, что человеческий ум так же, как механизм машины, сумеет выбрать в гуще комбинаций и расстановок всегда самый лучший ход, и что применение этого метода обеими сторонами приводит к ничьей.

Задача для коня 'магический квадрат': сумма чисел, из которых каждое определяет очередную позицию коня, по вертикальным и горизонтальным рядам составляет 260

"Ничейная теория" потерпела поражение благодаря мастерству Алехина, который разгромил Капабланку, блестяще выиграв у него партии и одерживая в своей долгой карьере многочисленные победы над сторонниками "ничьих". Алехин убедительно доказал, что комбинационные возможности на шахматной доске не будут исчерпаны до тех пор, пока в игре принимают участие живые люди.

Превосходная школа советских шахматистов, опираясь на традиции шахматной мысли Чигорина, бесповоротно опровергла точку зрения об "идеальной ничьей". Ряд побед на международной арене, достигнутых плеядой знаменитых советских шахматистов, таких, как чемпион мира Ботвинник, Бронштейн, Смыслов, Таль и многие другие, показал, что шахматная игра может быть динамичной, а отдельные встречи и коллективные турниры могут проходить остро, доставляя большие волнения как самим игрокам, так и наблюдателям.

Пять ферзей держат под ударом все клетки шахматного поля. Пример популярной задачи на расстановку шахматных фигур

Один из многочисленных способов расстановки на шахматной доске 8 ферзей таким образом, чтобы отдельные фигуры не могли бить друг друга

Нам известен только один "гарантированный" метод, обеспечивающий даже очень слабому игроку выигрыш, а в худшем случае ничью с мастером. Но это - уже снова область анекдота. Хитроумие здесь состоит в одновременном ведении игры на двух досках против двух противников при условии, что одна партия играется белыми, а другая - черными. Противник делает первый ход белыми. Этот же ход следует повторить на другой доске и подождать ответа. Движение черных по очереди мы повторяем на первой доске, ждем ответа, таким же образом производим ход против второго противника и так далее. Одна из этих двух партий, разыгранных по такой "системе", должна быть обязательно выиграна. Предполагаемую ничью одновременно с двумя мастерами можно также в каждом из случаев считать успехом.

Эта забавная идея двойной игры уже давно была темой анекдотов и рассказов. Так, например, есть рассказ русского автора В. Азова, описывающий неприятную историю, в которую попал Ласкер. Коротко эта история выглядит так: во время одного международного турнира к тогдашнему чемпиону мира Ласкеру обратился некий гражданин и заявил, что его сын - вундеркинд, "чудо-ребенок", подающий надежду стать шахматным гением. Отец "гения" предложил мастеру сыграть с его сыном только одну партию. Для облегчения дела он предложил провести розыгрыш в письмах. Ценя время мастера, он готов уплатить за проигранную сыном партию 500 долларов. Но дело не в деньгах: он хочет дать возможность своему ребенку сыграть с таким замечательным шахматистом. Если же однако (на что вообще он не рассчитывает), его сынок каким-то образом выиграет, Ласкер должен будет уплатить 2500 долларов. Не имея возможности отвязаться от нахала, надоедавшего ему каждый день в гостинице, Ласкер согласился. Сначала он пренебрегал противником, но, увидев, что партия принимает серьезный оборот, сосредоточился и с трудом выиграл. Отец "чудесного ребенка" сдержал слово и уплатил проигранные 500 долларов. А когда потом в беседе с Капабланкой Ласкер рассказал об этой истории, то раскрылась тайна игры. Оказывается, Ласкер играл партию с Капабланкой, а "чудесный ребенок" был лишь посредником в игре. Это стоило Капабланке 2500 долларов, а отец "гениального мальчика" получил чистую прибыль в сумме двух тысяч долларов.

В других версиях, приводимых в многочисленных анекдотах, розыгрыш "двойной" партии приписывается Алехину. Мастер попал в хитро поставленную ловушку. Он согласился играть на большую ставку с двумя неизвестными игроками на поставленных ими условиях. Вскоре оказалось, что игроки повторяют ходы Алехина на другой доске. Положение казалось безвыходным. В этом положении даже ничья принесла бы Алехину большую материальную потерю. Огорченный Алехин в какой-то момент сделал на одной из досок ошибочный ход. Противник, заметив это, решил дальше вести игру самостоятельно, чтобы добиться выигрыша и тем самым добиться победы на обеих досках. Однако такое отступление от принятого "железного" правила точного подражания ходам мастера привело к роковым последствиям. Алехин легко выиграл обе партии.

В этих анекдотах есть своя мораль. Оказывается, не стоит прибегать к холодным расчетам, выбирая способ выигрыша. Наученные этим опытом, мы не должны, садясь за игру, преувеличивать роли математического счета и расчета.