Дамка с простыми против простых

Пп. при Д., когда они действуют с ней в контакте, чрезвычайно повышают ее ударную силу.

№74. Баба Си - В. де Йонг Хогезанд, 1964

74. Об этом эндшпиле говорится в предисловии. Сенегалец сыграл 1.24 - 19?, в ответ на что Ч.... сдались! Впоследствии М. Изар и Г. Кремер показали за Ч. ничью: 1...31 2.32 (2.13 23! =) 2...36! (с жертвой п.18 надо выждать, пока Д. покинет поле 32. Объяснение этому в 79) 3.37 23 4.28 14 5.23 20 6.19 25, и эту п. задержать не удается. Итак, ход Баба Си 1.24 - 19, должен был привести к ничьей. К победе вело 1.37!

Знание приемов борьбы в эндшпилях, где Д. отрезает пп. по б. дор., особенно необходимо.

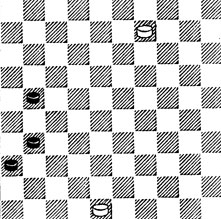
№75. Выигрыш

75. Б. выигрывают, так как после 1.3 27 2.14 32 3.26 41 следует 4.37 и 5.42 ×.

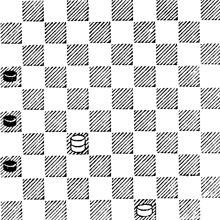
№76. Выигрыш

76. 1.23 (можно и 1.19 или 1.5, но не 1.46?) 1...31 2.43 21 3.38 (Б. подготовились к выходу Ч. п. на 27) 3...27 4. 23 - 32! × - у Ч. цугцванг.

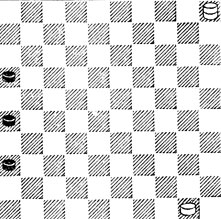
№77. Выигрыш

77. 1.44 31 2.39 21 3.33 27 4. 33 - 28! ×.

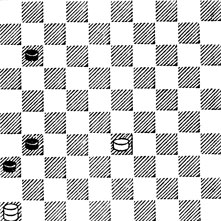
№78. И. Мертенс 1938. Выигрыш

78. Здесь идея выигрыша другая: 1.33 - 28 16 (1...17 2.22 ×) 2.22 21 3.23! 27 4.1 ×.

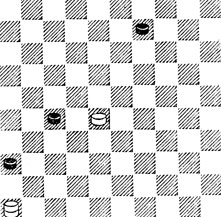
№79. К. Бланкенаар 1895. Из партии. Выигрыш

79. Ч. хотят перевести п. 9 через б. дор. Поэтому 1.23. Однако ценой жертвы Ч. добиваются своего - 1...32 2.28 14. Теперь немедленный марш п.23 в дамки бесполезен: Ч. п. прорвется. Но выигрыш все же есть: 3.32! Только сюда! 3...20 4.19! П. должна идти по б. дор. 4...25 5.14 30 6.10 34 7.5 39 8.49! ×.

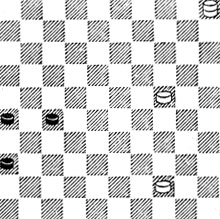
№80. Выигрыш

80. Предотвратить прорыв Ч. п. 36 в дамки нельзя: п. 44 стать на 28 (как в 77) не успевает. А нельзя ли в таком случае заранее подготовить петлю? 1.40! 26 - 31 2.35 32 3.26 41 4.42! (или 4.12) 4...47 5.29 × - Ч. в цугцванге.

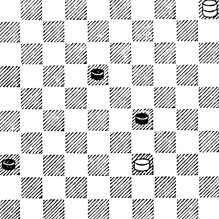
№81. В. ван Даален 1922. Выигрыш

81. Ч. угрожают перекрыть б. дор. (1...33 и 2...23) и двинуть п. 36. Как предотвратить ничью? Если 1.46, то 1...23 и 2...33. Все же выигрыш у Б. есть - 1.19! Остальное ясно.

Стой же п. не на 36, а на 31, Ч. спаслись бы, так как после 1.19 36 Б. в цугцванге: они сами должны разрушить выгодную для них позицию.

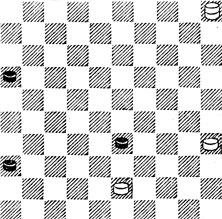
№82. Г. Лесаж 1895. Выигрыш

82. И тут Ч. угрожают перекрыть б. дор. ходом 1...38. Поэтому 1.46 21 2.30 27 (с угрозой 3...32 =) 3.10! 31 4.24! ×.

№83. Ничья

83. Если 1.37 46 2.31 37 3.19, то 3...42 4.13 19 и т. д. ×. И все же Б. могут уйти от поражения. 1.38. Куда пойдут Ч.? Если 1...46, то 2.31 и 3.32 с ничьей. Если 1...5 или 1...23, то 2.20, и угроза 3.32 с последующим 4.31 неотразима. Б. п. 20 прорывается в дамки.

№84. Б. Севастьянов 1929. Ничья

84. И в этом положении Б. могут сделать ничью. 1.15 23! (нейтрализуя угрозу 2.9 14 3.19 и 4.10 =) 2.20! 28 3.14 5 4.9 14 5.10 - ничья.

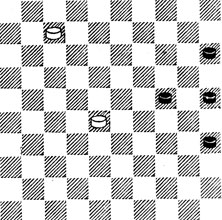
№85. И. Мертенс 1938. Выигрыш

85. 1.1. Ч. пп. отрезаны по верхнему двойнику. Такая же ситуация была в 60. Но там Б. п. отсутствовала и Д. с трудом добивалась ничьей. Здесь же наличие Б. п. делает Д. хозяйкой положения. 1...25 - 30 2.28 - 23. Иногда, как видите, полезно перекрыть диагональ, по которой действует своя Д. 2...20 3.7. Б. ждут, когда у Ч. иссякнут ходы. 3...25 4.19 13 5.1 ×. Возникла одна из немногих позиций, где одинокая Д. выигрывает у четырех пп.

№86. П. Лейг 1926. Выигрыш

86. Одна из Ч. пп. уже перешла двойник, но это их не спасает - 1.1 29 2.25 40 3.39 43 4.34 ×.

№87. И. Мертенс 1938. Выигрыш

87. Подобные окончания часто встречаются в игре. Б. выигрывают, осуществляя интересную идею. 1.6 20 2.11 25 3.50 35 - 40 4.6 33 5.35 39 (5...30 6.24 39 7.38 ×) 6.49 30 7.32 35 (7...34 8.49 ×; 7...44 8. 40 ×) 8.27! 44 9.22! ×.

В борьбе одинокой Д. против трех пп. наиболее частый исход - ничья. Но если силы сторон увеличить одинаково - на шашку, то шансы на выигрыш скорее приобретет Д. Это демонстрируют этюды одного из лучших композиторов на стоклеточной доске Н. И. Шеломенцева.

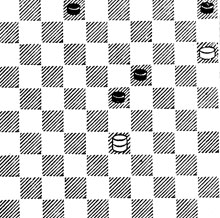
№88. Н. Шеломенцев 1970. Выигрыш

88. Этюд назван автором "вездесущая дамка". Если снять по Б. и Ч. шашке - будет ничья. Теперь же благодаря взаимодействию с п. активность Д. чрезвычайно возрастает.

1.17! 7 (А) 2.6! 12 3.33 18 4.17. Поле 17 привлекает Д., потому что отсюда она сможет быстро наладить контакт со своей п. 4...24 (если 4...29, то 5.8! 24 6.30 33 7.25 ×) 5.8! 24 - 29 6.3! ×. Угроза 7.10 неотразима.

А. 1...29 2.3 24 3.12! 33 4.17! 38 5.3 ×. Замечательный этюд, богатый тонкими маневрами действительно вездесущей Д.

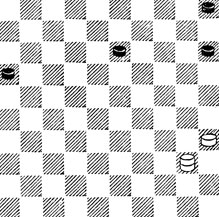
№89. Н. Шеломенцев 1970. Выигрыш

89. 1.30! 19 2.25. Чтобы взаимодействие Д. и п. осуществилось, эта п. сначала должна сблизиться с п. противника. 2...24 (угрожало 3. 35 и 4.20 ×) 3.12! 10 4.8 21 (если 4...29, то 5.24 и т. д. × - создается вилка) 5.35 14 6.8! 27 (6...26 7.13 15 - 20 8.4 24 9.15 ×) 7.26! 32 8.42 15 - 20 9.15 37 10.47 19 11.20 23 12.15 29 13.24 41 14.19 ×.

Здесь приведен лишь гл. вар. этого поучительного и сложного этюда. Тем, кто не боится заблудиться, рекомендую побродить в дебрях его многочисленных ответвлений.

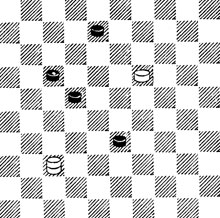
№90. Н. Шеломенцев 1970. Выигрыш

90. Когда Д. и п. борются с несколькими пп., бывает возможно жертвой шашки вскрыть недостатки в расположении этих пп. Тут пп. 17 и 22 находятся в состоянии самоблокады. Но как это использовать? 1.42! 39 2.13! 19 3.26 ×.

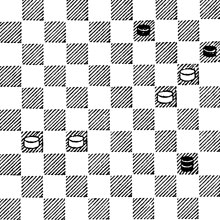
№91. Н. Шеломенцев и А. Сафроненко 1970. Ничья

91. Находиться в самоблокаде - удел не только пп., иногда в ней оказываются и ДД. Здесь Б. добиваются ничьей, вызывая такую расстановку Ч. шашек, что из-за самоблокады их Д. не может избежать размена.

1.28! 12 (1...35 2.14! =) 2.22! Б. пп. намерены создать для Ч. Д. угрозу размена. Как играть Ч.? Если 2...26, то 3.18 и 4.14 =. Но 2...3! выглядит выигрывающим - ведь стоит угроза 3...14 ×. Однако спасение у Б. есть! 3.19! 13 4.26 с ничьей: размен Ч. Д. неминуем.

Завершая этот раздел, рассмотрим еще ряд примеров на такие важные и часто встречающиеся в окончаниях темы, как трамплин, цугцванг, идея Эмбдена, идея Ианури.

Создание трамплина является одним из эффективнейших приемов взаимодействия Д. и п. Вот пример.

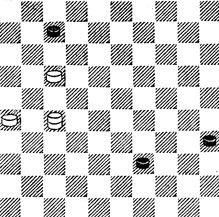
№92. Выигрыш

92. Ч. пп. далеко продвинулись и без трамплина выиграть не удалось бы. 1.11! 16 2.26 - 21 - подобное запирание п. и есть трамплин. Он намного увеличивает ударную силу Д. Вот и здесь - от угрозы 3.36 защиты у Ч. нет.

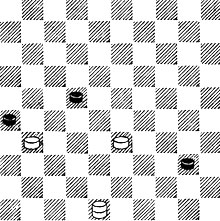
№93. Р. Бергсма 1947. Выигрыш

93. Ч. п. 26 наводит Б. на мысль о трамплине. Но если сразу 1.37, то Ч., конечно, не ответят 1...44 или 1...45 (ввиду 2.33 - 28 и 3.46 ×), а разрушат трамплин ходом 1...27. Поэтому - 1. 28! 33, а теперь создать трамплин - 2.37 ×.

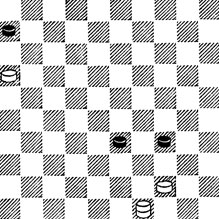
№94. А. де Йонг 1938. Из партии. Ход черных

94. После, казалось бы, дающего ничью 1...34 - 39 и 2.40 44 следует 3.21! 35 4.17! 38 5.16 - 11 - трамплин! Ч. сдались.

№95. И. Вейс 1934. Выигрыш

95. Выиграть помогает трамплин - 1.41! 36 (1...25 2.36 ×) 2.23 25 (2...24 3.19 20 4.14 ×) 3.34 ×.

Теперь о цугцванге. К сожалению, ошибочное толкование этого важного приема встречается даже в книгах. В одной читаем: "Цугцвангом называют позиции, в которых любой ход ведет- к поражению"; в другой: "Этот термин обозначает внешне хорошее положение, в котором нет удовлетворительных ходов". Не удивительно, что после таких определений авторы демонстрируют в примерах не цугцванг, а как раз противоположное ему понятие - неотразимую угрозу...

Что же такое цугцванг? Если сторона при своей очереди хода неизбежно терпит урон, то это может быть по двум причинам: либо противник создал угрозу, которую нельзя удовлетворительно отразить, либо угрозы нет (и потому отражать ничего не надо!), а потери вызываются лишь обязанностью сделать ход. Вторая ситуация и есть цугцванг.

В дебюте и миттельшпиле он наблюдается редко, но в эндшпиле значение его возрастает. "На молекулярном уровне" примером цугцванга является оппозиция - Б. п. 32; Ч. п. 22. Ход Ч. Угроза им есть? Нет. Почему они проигрывают? Только из-за обязанности сделать ход.

Нередко в окончании с ДД. имеющий преимущество старается лишь создавать угрозы. И создает... Но каждая отражается, и партия завершается вничью. К цели же привел бы цугцванг. Простой пример - цепочка. Б. Д. 2; Ч. пп. 22, 33. Б. могут создать угрозы, сыграв а) 1.24, б) 1.13, в) 1.11. Но пользы от них не будет! А как выиграть? Надо, не угрожая ничем, создать у Ч. цугцванг - 1.16! И теперь обязанность сделать ход убийственна для Ч.: 1...28 2.43 ×; 1...39 2. 11 ×.

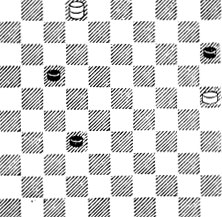
№96. Выигрыш

96. В этой позиции из партии немедленное 1.24? (с прицелом на трамплин) дало бы лишь ничью: 1...22! 2.25 - 20 28, и Б. оказались бы в цугцванге. К победе же ведет предварительное 1.8!, благодаря чему Б. выигрывают темп. Теперь - 1...22 2.24 28 3. 25 - 20, и в цугцванге уже Ч.! Им ничто не угрожает, но они проигрывают. Почему? Потому что обязаны сделать ход!

Позиции, где выигрыш достигается созданием цугцванга, уже вам встречались (например, 76, 80, 81) и еще немало их встретится впереди.

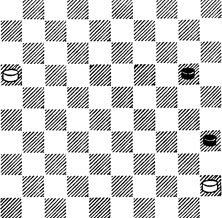
№97. Выигрыш

97. Как выиграть в этой и подобных позициях, еще в 1785 году указал голландец Е. ван Эмбден. 1.11 24 2.7 29 3.2 33 4.16 - заставляя Ч. п. идти к полю 44. 4...39 5. 21! Выжидательный ход. 5...44 6.17! ×. Так было и в 87.

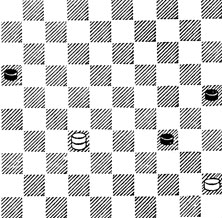
№98. А. де Йонг 1936. Выигрыш

98. Б. используют идею ван Эмбдена - 1.43 30 2.48 21 3.43 26 4.48. Ч. должны жертвовать. 4...31 5.26 39 6.21 35 (6...44 7.40 ×) 7. 16! 44 8.11 ×.

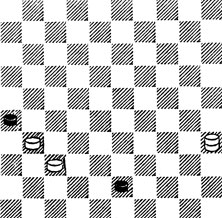
№99. Выигрыш

99. Эту идею выигрыша показал в 1787 году один из "первопроходцев" шашечной теории - француз К. Манури: 1.49! 48 2.21!! 17 3.26 31 4. 37 ×.

№100. Блонд 1800. Выигрыш

100. Здесь идея Манури применяется при Ч. п., запертой не на 26, а на 15. 1.9 31 2.4 36 (2...37 3.19 ×) 3.27 41 4. 32! 47 5.10! ×.

№101. Д. Вирсма 1926. Выигрыш

101. 1.3 32 (Б. угрожали завладеть б. дор. Если же 1...34 2.29 32, то 3.14 38 4.37 ×) 2.14! 38 3.25 35 4.48 31 5.26 43 6.48! 49 7.30! 24 8.35 ×.