Еще одна словесная головоломка

Когда вы решаете крисс-кросс, вам дана не только клеточная структура, но даны также слова, которые предстоит вписать. Другой тип головоломок отличается тем, что вам предоставляется право самим выбирать слова, которые вы будете вписывать. С одной стороны, это упрощает вашу задачу, так как вы получаете больше свободы. С другой стороны, наличие списка слов в крисс-кроссе облегчает его решение, так как позволяет применять метод отсечений. Когда клеточная структура содержит много пересечений, головоломки обоих типов бывают довольно трудны.

Иногда в некоторые клетки буквы вписаны заранее. Это опять-таки, с одной стороны, ограничивает вашу свободу, а с другой - позволяет от чего-то оттолкнуться при решении.

Чем больше пересечений в схеме, тем труднее задача. Сложнее всего вписывать слова в прямоугольники, когда каждое слово пересекается со всеми остальными. Пример такой задачи на рис. 102.

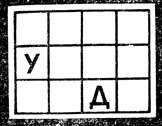
Рис. 102

Попробуйте заполнить буквами свободные клетки так, чтобы в каждом столбце и в каждой строке было записано какое-нибудь слово. Все слова, конечно, должны быть различны. При этом слова в столбцах должны читаться сверху вниз, а в строках - слева направо. Кроме того, налагаются обычные ограничения: запрещаются имена собственные, сложносокращенные слова, состоящие из одних заглавных букв, и т. д.

Решение, известное автору, таково (рис. 103).

Рис. 103

Оно - не единственное. Например, можно и так (рис. 104).

Рис. 104

Возможно, вам удастся придумать что-нибудь другое. Вообще в задачах такого рода единственность решения гарантировать практически невозможно, так как запас слов четко не очерчен.

Естественный интерес представляет задача о том, какова максимальная площадь прямоугольника, в клетки которого возможно вписать буквы так, чтобы в столбцах и строках образовались различные слова. В частности, интересно было бы найти решения для квадратов возможно большего размера. На рис. 105, а, б и в приведены примеры заполнения квадратов 2×2, 3×3 и 4×4. Что касается квадрата 5×5, то уже для него автору решение неизвестно.

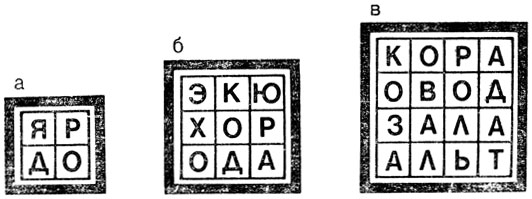
Рис. 105

Конечно, подобные задачи могут оказаться непростыми не только в случае прямоугольных клеточных структур. Две задачи с непрямоугольными схемами приведены на рис. 106. Они разрешимы, в чем читатель убедится, посмотрев на рис. 107.

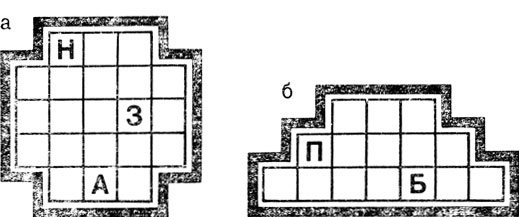
Рис. 106

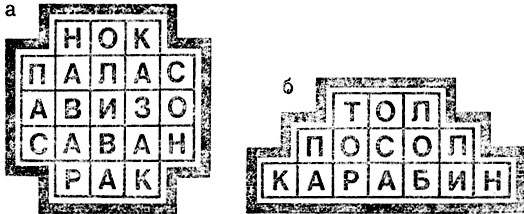
Рис. 107

Существуют ли другие решения?