"Крестики-нолики"

В стандартные "крестики-нолики" (тик-так-тоу) играют на доске 3×3 клетки. Игроки поочередно выставляют свои символы в свободные клетки доски: один выставляет крестики, другой - нолики. Начинают крестики. Побеждает тот, кто первым построит ряд (по горизонтали, вертикали или диагонали) из своих символов. Эта простейшая игра знакома, видимо, всем читателям, - кто же не играл в нее в детстве? Многие, если не все, читатели знают также, что при правильной игре обеих сторон партия кончается вничью: к моменту заполнения всех клеток доски ни одному из соперников не удается построить ряд.

Интересно, что есть масса игр, по существу совпадающих с тик-так-тоу, но только так, что совпадение это замаскировано и сразу догадаться о нем трудно. Вот несколько известных примеров (возможно, читателю они уже знакомы, поскольку приведены в книге М. Гарднера "Математические новеллы").

Имеется колода карт, на каждой из которых стоит одно из чисел 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего в колоде 9 карт, и все они различны. Игроки поочередно выбирают из колоды по одной карте (при этом все карты на виду и брать можно свободно). Выигрывает тот, кто первым наберет три карты так, что сумма чисел на них будет равна 15. Такова первая игра из трех, которые мы рассмотрим.

На первый взгляд, что общего у нее с тик-так-тоу? Тем не менее на самом деле тик-так-тоу и описанная игра с числами идентичны, просто в игре с числами правила тик-так-тоу излагаются как бы на другом языке. Сейчас мы поясним, что это конкретно означает.

Давайте нарисуем на доске тик-так-тоу следующий магический квадрат (рис. 58).

Рис. 58

В его клетках стоят числа от 1 до 9, т. е. как бы карты нашей колоды, а сумма трех чисел в каждом ряду (горизонтальном, вертикальном или диагональном) как раз равна 15, так что всякому ряду соответствует набор трех карт, дающих в сумме 15. С другой стороны, каждому представлению числа 15 в виде суммы трех различных целых чисел от 1 до 9 соответствует ряд магического квадрата, изображающий это представление. Поэтому набрать три карты так, чтобы они дали в сумме 15, - это в точности то же самое, что набрать тройку карт, стоящих в одном ряду квадрата. А это уже задача игры в тик-так-тоу!

Итак, как играть в предложенную игру с числами? Очень просто: когда противник берет карту, ставьте символ противника в клетку квадрата, где написано число, стоящее на взятой карте, затем определяйте, какой ход в "крестики-нолики" следует сделать, и берите карту с номером, написанным в той клетке, куда вы ставите свой символ.

А вот вторая игра - с совершенно иным "игровым материалом". Придумал ее Л. Мозер.

Имеется колода из 9 карточек, на каждой из которых написано одно из слов: рыба, клин, нить, небо, сок, бусы, тор, сеть, река. Написанные на разных карточках слова различны. Карточки лежат заполненной стороной вверх. Игроки поочередно берут себе по одной карточке. Цель игры - первым набрать три карточки со словами, имеющими общую букву.

Чтобы понять, почему игра Мозера совпадает с тик-так-тоу, запишем 9 слов в клетках доски 3×3 следующим образом (рис. 59).

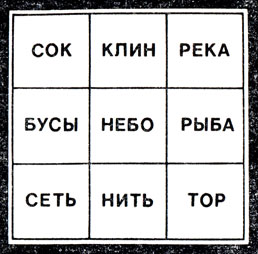
Рис. 59

Видно, что любые три слова из одного ряда имеют общую букву и в то же время никакие три слова, не стоящие в одном ряду, не имеют общих букв. Поэтому набрать тройку карточек так, чтобы написанные на них слова имели общую букву, - это то же самое, что взять тройку карточек из одного ряда. Это снова задача игры в тик-так-тоу.

Наконец, посмотрите на игру, придуманную голландским психологом Дж.-А. Мишоном. Она называется "пробка". На рис. 60 изображена карта, где показаны города (они обозначены кружками) и связывающие их дороги. Все дороги занумерованы. Двое участников поочередно закрашивают какую-то из еще не закрашенных дорог в свой цвет на всем ее протяжении; при этом нельзя красить дорогу, пересекающую какую-либо из закрашенных. Выигрывает тот, кто первым закрасит в свой цвет три дороги, ведущие в какой-либо город.

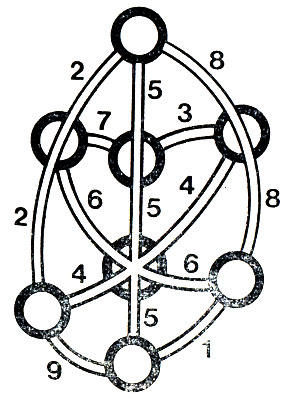
Рис. 60

Оказывается, что и эта игра не что иное, как переформулированные "крестики-нолики". Карту, изображенную на предыдущем рисунке, можно перерисовать так (рис. 61).

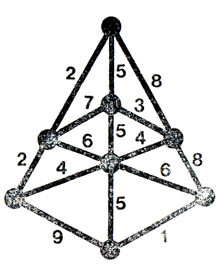
Рис. 61

Здесь точки обозначают города, а прямые линии - дороги. Числа рядом с линиями - это номера дорог. Посмотрите на этот рисунок, а затем на рис. 58. Не замечаете ли вы, что каждому ряду магического квадрата соответствует город, в который ведут дороги с номерами, указанными в этом ряду квадрата?

Это действительно так, причем верно и обратное: каждому городу соответствует ряд магического квадрата, в котором стоят как раз номера дорог, ведущих в этот город. Ну, а раз так, то закрасить в свой цвет три дороги, ведущие в какой-либо город, - это то же самое, что поставить три своих символа в ряд на доске 3×3. Стало быть, "пробка" - всё те же "крестики-нолики".

Игра тик-так-тоу обратима: существуют обратные "крестики-нолики", правила которых не отличаются от правил стандартных "крестиков-ноликов", но цель противоположна - заставить противника построить три своих символа в ряд. Крестики, т. е. сторона, ходящая первой, могут обеспечить себе ничью: надо первый ход сделать в центр, а затем симметрично повторять ходы противника. С другой стороны, можно убедиться, что обеспечить себе победу крестики (при оптимальной игре ноликов) не могут. Поэтому правильный исход партии в обратные "крестики-нолики" - ничья.

В так называемых безумных "крестиках-ноликах", которые были предложены А. К. Остином, оба игрока могут выставлять в свободные клетки доски как крестики, так и нолики (не напоминает ли это читателю ставропольские шашки?) по своему усмотрению, а цель состоит в том, чтобы первым построить ряд из трех одинаковых символов. Оказывается, что здесь побеждает ходящий первым. Вот как он это делает.

Первым ходом надо поставить крестик (можно и нолик, но мы ограничимся изложением одного из способов выигрыша) в центр доски. На это второй игрок должен выставить нолик, иначе он сразу проиграет. Если он выставит нолик в угловую клетку, первый игрок рисует нолик в симметричной относительно центра угловой клетке, после чего на любой ответ он сможет закончить ряд из трех одинаковых символов. Если же второй игрок в ответ на ход в центр нарисует нолик не в угловой клетке, следует также нарисовать нолик симметрично. Теперь второй игрок еще может безопасно поставить нолик в неугловую клетку, но после симметричного ответа первого игрока он окажется в цугцванге.

Любопытно, что обратные безумные "крестики-нолики" - снова игра ничейная, как было показано Р. Эбботом.

Д. Сильвермен предложил игру, правила которой совпадают с правилами стандартных "крестиков-ноликов", но в которой целью одного игрока является добиться ничьей, а целью другого - избежать ее. Можно показать, что тот, чья цель - избежать ничьей, имеет выигрывающую стратегию, независимо от того, ходит ли он первым или вторым.

Игровое поле 3×3, конечно, очень мало, и в любых разновидностях "крестиков-ноликов" на этом поле можно разобраться до конца. Интереснее других разновидности, в которых используются большие игровые поля. Среди них самой популярной является игра "пять в ряд", которая отличается от стандартных "крестиков-ноликов" тем, что:

1) игровое поле бесконечно (на практике это означает, что оно так велико, как это требуется игрокам);

2) для достижения победы надо выставить в ряд не три своих символа, а пять.

В этой игре крестики имеют, как утверждают знатоки, решающее преимущество (впрочем, насколько известно автору, полное доказательство этого ни в одной книге не приводится). Однако она достаточно сложна, и на практике все зависит от сил соперников.