Так-тикль

Игра с забавным названием так-тикль входит в состав хорошо известного комплекта "Наша игротека". Появилась она недавно и представляет собой своеобразный гибрид шашек и "крестиков-ноликов". Для игры в так-тикль используется доска 4×4, на которой расставлены 4 белые фишки и 4 черные фишки так, как показано на рис. 10.

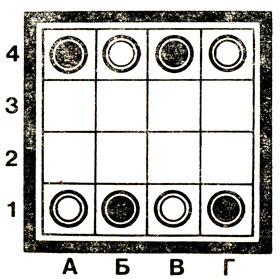
Рис. 10

Ходы делаются по очереди. Начинают белые. За один ход можно передвинуть любую из своих фишек на одну клетку по горизонтали или по вертикали, если она оказывается при этом на свободном поле. По диагонали ходить нельзя. Цель игры - выставить тройку своих фишек в ряд по горизонтали, вертикали или диагонали, как в "крестиках-ноликах". Кто первым сделал это, тот победил.

Е. Я. Гик в своей книге "Занимательные математические игры", упоминая о так-тикле, пишет, как с помощью ЭВМ было доказано, что игра ничейная: при правильной игре обеих сторон ни одной из них не удается построить ряд из трех фишек своего цвета. Здесь мы расскажем, как именно должны действовать обе стороны, чтобы добиться ничьей. Ничейный вариант, который будет изложен, был найден автором без помощи ЭВМ.

Оптимальная партия

В начальной позиции белые имеют по существу две возможности: 1. А1-А2 и 1. В1-В2. На первый взгляд 1. В1-В2 сильнее, так как способствует обладанию центром. На самом деле этот ход быстро проигрывает. Ответ 1 ... Г1-В1 создает угрозу сыграть Б1-Б2 и А4-А3×, от которой можно защищаться путем 2. А1-А2, 2. Б4-Б3, 2. В2-Б2 и 2. Г4-Г3, но ни одна из этих защит не спасает. Если 2. А1-А2, то 2 ... Б1-Б2. 3. А2-А3 В4-В3 и белые не могут воспрепятствовать маневру В1-Б1-А1×. Если 2. Б4-Б3, то 2 ... Б1-Б2. 3. Б3-А3 Б2-Б3 с неизбежным 4 ... Б3-Б4×. Если 2. В2-Б2, то 2 ... В4-В3 и 3... В1-В2, после чего неизбежно 4 ... Б1-В1×. Если 2. Г4-Г3, то 2 ... А4-А3. 3. В2-Б2 В4-В3 и снова нет защиты от 4 ... В1-В2 и 5... Б1-В1×.

Таким образом, лишь ход 1. А1-А2 требует изучения. В ответ на него у черных есть четыре возможности; но видно, что две из них сразу проигрывают:

- 1 ... А4-А3? 2. А2-Б2, и теперь если 2 ... А3-А4, то 3. Б4-Б3 В4-В3. 4. Г4-В4 и 5. Б2-А2Х; если 2 ... А3-А2, то 3. Б4-Б3 В4-В3. 4. Г4-В4 и 5. В4-Б4×; если 2 ... А3-Б3, то 3. Б4-А4 Б3-А3. 4. Б2-Б3 и 5. В1-В2×; если 2 ... Б1-А1, то 3. Б4-Б3 и либо 4. Б3-В3×, либо 4. В1-Б1×; если 2 ... В4-В3, то 3. Б4-Б3 с неизбежным Г4-В4-Б4×; если 2 ... Г1-Г2, то 3. Б4-Б3 В4-В3. 4. Г4-В3 и 5. В4-Б4×;

- 1 ... В4-В3? 2. Б4-Б3 В3-В4. 3. Б3-Б2 и 4. В1-В2×.

Поэтому внимания заслуживают лишь ответы 1 ... Б1-Б2 и 1 ... Г1-Г2. Начнем с 1 ... Б1-Б2 - это и есть верный ход.

На 1 ... Б1-Б2 белые обязательно должны играть 2. Б4-Б3. Все остальные ответы проигрывают:

- 2. А2-А3? В4-В3. 3. В1-В2 (иначе черные сыграют 3 ... В3-В2 с победой) Г1-В1, и от рейда В1-Б1-А1 нет защиты;

- 2. А2-А1? В4-В3 и либо 3 ... Б2-Б3 и 4 ... А4-А3×, либо 3 ... В3-В2 и 4 ... Г1-Г2×;

- 2. В1-Б1? А4-А3. 3. Б1-В1 Б2-Б3 и 4 ... В4-В3×;

- 2. В1- В2? А4-А4. 3. В2-В1 Б2-Б3 и 4 ... В4-В3×;

- 2. Г4-Г3? В4-В3. 3. В1-В2 А4-А3 или 3. Б4-Б3 Г1-Г2 с победой черных.

Итак, 2. Б4-Б3. На это правильный ответ - 2 ... А4-А3. В свою очередь белые могут отвечать лишь 3. Г4-Г3, поскольку фишки В1 и Б3 трогать нельзя, а на 2. А2-А1? выигрывает 3 ... Б2-А2 с неизбежным В4-Б4-А4 ×. После же правильного 3. Г4-Г3 черные не могут ходить фишкой Б2. Не могут они также ответить 3 ... А3-А4? из-за 4. Б3-А3 с неизбежным В1-Б1-А1×. Ходы 3 ... В4-Б4? и 3 ... В4-Г4? проигрывают одинаково: следует 4. Г3-В3 Б4-В4 (во втором случае Г4-В4) и 5. А2-А1. Теперь нельзя играть фишкой В4 из-за 6. В3-В2 и 7. Б3-В3×, а также фишкой Г1 из-за 6. В3-В2 с двойным ударом. "Прикована" и фишка Б2. На 5 ... А3-А4 выигрывает 6. А1-Б1 А4-А3 (грозило 7. В1-В2 и 8. В3-Г3×). 7. В3-Г3 Б2-В2. 8. Б1-Б2 и 9. В1-Б1×. То же самое происходит в случае 5 ... А3-А2. Таким образом, осталось рассмотреть ходы 3 ... Г1-Г2 и 3 ... В4-В3.

Начнем с 3 ... Г1-Г2. На это белые играют 4. В1-В2 (между прочим, это единственный ход - все другие проигрывают). В4-В3. 5. Г3-Г4 В3-В4. 6. В2-В3, и после вынужденного 6 ... Г2-Г3 возникает позиция, которая столь важна, что заслуживает особого названия. Я называю ее "змейкой". Она изображена на рис. 11.

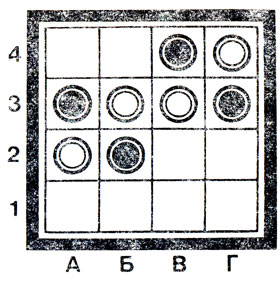
Рис. 11

Если бы сейчас ход был черных, белые выиграли бы немедленно. Замечательно, что и при своем ходе белые побеждают. Вот что происходит: 7. А2-А1! - белая фишка отправляется в далекое путешествие - 7 ... А3-А2 (нельзя трогать фишки Б2 и Г3, на 7 ... В4-Б4 следует 8. Г4-В4 Б2-А2. 9. Б3-Б2×, а на 7 ... А3-А4 выигрывает тот же маневр, что и на 7 ... А3-А2, но все кончается еще быстрее). 8. А1-Б1 А2-А1 (если 8 ... А2-А3, то 9. Б1-В1 и 10. В3-В2 - это и есть суть маневра белых). 9. Б1-В1 В4-Б4 (иначе 10. В3-В2). 10. В1-В2 Б4-В4. 11. Б3-Б4 Г3-Г2. 12. Г4-Г3 Б2-Б3. 13. В2-Б2 В4-Г4. 14. Б2-Б1 Г2-В2 15. Г3-Г2×. Так выигрывает 7. А2-А1. Тем самым показано, что проигрывает 3 ... Г1-Г2.

Наконец, рассмотрим 3 ... В4-В3. Это и есть обещанная ничья. Белые могут форсировать повторение ходов: 4. Г3-Г4 В3-В4. 5. Г4-Г3 и т. д.

Ничего другого у них нет: на 4. А2-А1? или 4. Г3-Г2? выигрывает 4 ... В3-В2.

Могут ли черные сыграть сильнее? Во-первых, рассмотрим альтернативы ходу 2 ... А4-А3. Если 2 ... А4-Б4?, то 3. В1-В2 с неотразимой угрозой 4. В2-В3. Очевидно также, что нельзя трогать фишку В4. На 2 ... Б2-Б1? выигрывает 3. Б3-Б2, а на 2 ... Б2-В1? - 3. А2-Б2. Наконец, если 2 ... Г1-Г2?, то 3. В1-В2 (кстати, остальные ходы проигрывают), после чего внимания заслуживают лишь ходы 3 ... А4-А3 и 3 ... Г2-Г3. Но на 3 ... А4-А3 белые играют 4. В2-В3, сводя игру к "змейке". Если же 3 ... Г2-Г3, то 4. В2-В3 опять позволяет белым получить "змейку" Таким образом, ход 2 ... А4-А3 действительно необходим.

Во-вторых, черные могли уклониться на первом ходу, сыграв 1 ... Г1-Г2. Оказывается, что это проигрывает. Белым следует ответить 2. В1-В2 и на любой ход черных 3. Б4-Б3. Именно:

- 2 ... А4-А3. 3. Б4-Б3 Б1-Б2. 4. В2-В3 с получением "змейки";

- 2 ... Б1-А1 (или 2 ... Б1-В1). 3. Б4-Б3 и 4 Б3-Б2×;

- 2 ... Б1-Б2. 3. Б4-Б3, и построение "змейки" неизбежно;

- 2 ... В4-В3. 3. Б4-Б3 с двойным ударом;

- 2 ... Г2-Г1. 3. Б4-Б3 Б1-Б2. 4. В2-В3 с двойным ударом;

- 2 ... Г2-Г3. 3. Б4-Б3 Б1-Б2. 4. В2-В3 А4-А3 - получилась "змейка".

Итак, правильная партия в так-тикль такова: 1. А1-А2 (возможна также симметричная партия, начинающаяся ходом 1. Г4-Г3) Б1-Б2. 2. Б4-Б3 А4-А3. 3. Г4-Г3 В4-В3. 4. Г3-Г4 В3-В4 - ничья повторением ходов. Любое уклонение от нее ведет к проигрышу уклонившейся стороны.