3. Словам тесно - мыслям просторно

Перейдем к разбору важных примеров с минимальным количеством сил. Если вы думаете, что это характеризует их простоту, то глубоко ошибаетесь: чем меньше шашек, тем глубже, ответственней и труднее расчет.

Диаграмма 26. Ход белых

Превосходство белых в положении на диаграмме 26 очевидно. У сил черных нарушено взаимодействие. Оппозиция, как легко убедиться, в пользу белых. Это дает основание искать путь к выигрышу.

1. cd4. Занимая центр, мы еще больше стесняем действия соперника. 1... аb6.

Интересно, что после 1...fe7 решает 2. de5, а напрашивающийся 2. dc5 дает возможность черным успешно защититься: 2...ef6

3. cd6 ab6 4. cd2 fg5 5. de3 gh4 (или 5... gf4 6. e:g5 ba5, и прорыв неминуем) 6. ef4 ba5 = .

2. cd2!

Казалось, есть возможность продолжать стеснять силы черных ходом 2. de5. В действительности такой план упускает победу: 2...fg7! 3. ed6 (после 3. cb2 bс5 4. bа3 к ничьей ведет любой из трех ходов: 4 ... gh6, 4 ... gf6, 4 ... cd4) 3... gf 6 4. cd2 fg5 5. de3 gh4 (или gf4) 6. ef4 ba5 и т. д. Белые выиграть не могут.

А вот после 2. cd2! белые занимают оппозицию.

Почему же нельзя допустить перестановку ходов, избрав сначала 1. cd2, а затем 2. cd4?. Подумайте!

В этом случае черные отвечают 1 - fe7, восстанавливают взаимодействие сил и уравнивают позицию.

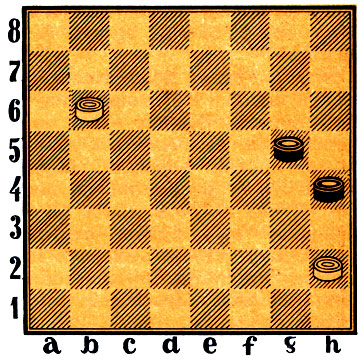
Диаграмма 27. Ход белых

Разве можно добиться успеха в таком положении, как показано на диаграмме 27? Обе стороны пробиваются в дамки, и ничья должна быть закономерным итогом борьбы. Но это поверхностная оценка. Сначала испытайте свою смекалку (с идеей вы уже знакомы) и лишь потом проверьте ответ. Кстати, к такому методу надо прибегать как можно чаще.

1. bc7 gf4 2. cd8! fe3 (единственный ход) 3. da5 ef2 4. ab6 fgl (4...fel 5. bf2 ×)5. ba7, и черные биты.

Диаграмма 28. Ход белых

Здесь (см. диаграмму 28) все очень просто. Белые выигрывают. Но как?!

1. ef8. Собственно, в этом ходе - существо примера. Теперь нельзя 1 - de3 из-за 2. cd8 с неотразимой угрозой 3. fg7. А если 1... dc3, то жертвуется дамка 2. fb4 с:а5 3. cb8 hg7 (иначе 4. be5 ×) 4. bе5 gh6 5. ес3 (только так!) 5... hg5 6. cd2 gh4 7! de1 - блокада (распорка).

Диаграмма 29. Ход белых

Диаграмма 29: 1. hg7 ed4 2. gh8 de3 3. gf4 e:g5 4. hd4 gf4 (h4) 5. df2 ×.

Но есть и другой путь: 3. hc3 ab6 4. ee1.

К победе ведет только такой маневр. Если 4. са5, то 4... bс5, и черные уходят от поражения.

4... bс5 (4... bа5 5. ес3 ×; 4... ef 2 5. еа5 ×) 5. еа5 cd4 6. ab4x.

На практике нередко бывает, что к цели ведут два или несколько путей. Но всегда надо стремиться к самому четкому и самому простому плану, ибо зачастую ложными оказываются варианты на первый взгляд приемлемые.

Диаграмма 30. Ход белых

Пример, показанный на диаграмме 30, перекликается с предыдущим. Чтобы успешно справиться с ним, нужен расчет на восемь ходов вперед: 1. cd6 ab6 2. de7 bс5 3. ef8 cd4 4. fg7 de3 5. gh6 ef2 6. hg3 f:h4 7. hf4 ba7 8. fc7.

В этом примере другой путь оказывается ложным: 4. fb4 de3 5. hg3 bc7 6. bс3 cd6! 7. ca5 (7. ee1 de5 =) 7 ... dc5!, и белые выиграть не могут.

Диаграмма 31. Ход белых

Как подойти к решению проблем, стоящих перед белыми в такой ситуации, как на диаграмме 31?

Когда остается мало шашек, хочется, и это совершенно естественно, определить, каково соотношение темпов, в чью пользу оппозиция. Вообще говоря, соотношение темпов всегда важно, а в симметричных и в почти симметричных позициях, в позициях с возможным окружением сил соперника оно может играть решающую роль. Но когда на доске шашек много и возможностей у сторон много, обнаружить решающее значение темпа очень трудно. При малом же количестве сил этот метод легко приложим.

Итак, количество нечетных шашек четно (1 и 7), следовательно, позиция четная. В оппозицию попадает тот, чей ход.

Простой размен передаст это преимущество белым. Но черные всеми силами будут избегать размена. Однако установленный нами факт дает возможность войти в непосредственный контакт с силами соперника и ограничить его действия. Пожалуй, любой, научившийся сколько-нибудь мыслить по-шашечному, сумеет самостоятельно провести подобное рассуждение. Больше того, он определит, что из двух ходов, дающих возможность войти в соприкосновение с силами черных, годится только один: fe5.

Мы иногда умышленно не будем доводить рассуждения до логического завершения, чтобы дать возможность сделать это самим читателям и приобщить их к анализу и мышлению.

1. fe5! fg7 (единственный ход). А что дальше? Решающий бой развернется на правом фланге. Казалось, ясно, что туда надо направить шашку "e1". Так, по-видимому, рассудила бы ЭВМ или человек, мыслящий трафаретно. Мы уже знаем, что при оппозиции обе стороны имеют равное количество шашек. Но бывают и такие случаи, когда одну активную шашку едва удается удержать с помощью двух боевых единиц.

Прежде всего убедитесь, что рейд простой "e1" на е3 или g3 приводит лишь к ничьей. К победе же ведет несколько парадоксальное 2. ed2! gh6 3. dc3! hg5 4. ef6 ed6 (если бы белая "с3" находилась на е3, то простая черная "d6" прорвалась бы в дамки) 5. f:h4 de5 6. hg5. Только усилия двух шашек на разных флангах привели к успеху.

Как ни просто только что разобранное, найти его совсем нелегко.

Диаграмма 32. Ход черных

Положение, приведенное на диаграмме 32, взято из партии, сыгранной на высшем шашечном форуме в финале XXII чемпионата СССР.

Казалось бы, чего проще? Развивай шашки левого фланга, занимай центр. Так думали и черные, избрав 1... fe5?. Но это ошибка: 2. hg5 ed4 3. gf2 dc5 4. ba3 dc3 5.fe3 fe7 6. gh6 ef6 7. ef4. Белые прорвались в дамки, и партия закончилась вничью.

Значит ли, что в исходной позиции надежд на выигрыш не было? Ведь черные играли как будто лучшим образом. Но все было бы смешно, когда бы не было так грустно! Игравший черными мастер не понял, что оппозиция в его пользу! И все потому, что обычно оппозицию подсчитывают, когда на доске остается только по одной или по две шашки...

К победе вело 1... de5! Это раскрепощает простую "f8" и дает возможность овладеть важным пунктом f4: 2. bс3 fe7! (пункт f4 уже в руках черных, но форсировать овладение им было бы ошибкой, так как сначала надо обезопасить намерения белых прорваться шашкой "с3") 3. cb4 ed6 4. ba5 dc5 5. gf2 ef4 ×.

Диаграмма 33. Ход белых

Новый пример (диаграмма 33) интересен тем, что белые на определенном этапе сами гонят черных ближе к дамочным полям.

1. ed8 cd6 2. fg7 fg3.

Не спасают и другие продолжения. Если 2... dc5, то 3. gh8 (или dh4) fеЗ 4. dh4 ed2 5. ЬсЗ и 6.hf 6 ×.

При 2... fe3 следует 3. db6 ed2 4. bе3 d:f4 5. gf8 и т. д. с выигрышем. Можно и 3. dg5 ef2 4. ge3 f:d4 5. gf8 и т. д. В обоих случаях возникает уже знакомое самоограничение.

3. dh4! gh2 4. hg3! h:f4 5. gf8, и черные не могут уйти от поражения.

На диаграмме 34 все кажется очень простым. Конечно, белые должны победить. Но попробуйте найти тропинку к цели.

Диаграмма 34. Ход белых

Исследуем ход 1. ef8. У черных два ответа. Если 1... ef4, то 2. fd6 fe3 3. dg3 ab4 (3... ed2 4. bс3 и 5. ge5) 4. ge1 ba3 5. bс3 ed2 6. cb4 × (или 6. eh4 и 7. hf6 ×).

Все получилось? Нет! В ответ на 1. ef8 следует 1... cd4, и выиграть белые не могут.

Остается 1. ed8. Теперь, если 1...ef4, то 2. dc7 fe3 3. cg3, и дальнейшее вы уже знаете. Не спасает и 1...ed4 2. df6! de3. 3. fh4 и т. д.

Хорошо ли вы усваиваете материал? Чтобы убедиться в этом, решите позицию мастера В. Кочарова. По существу в ней подобная идея. В определенный момент надо заставить черных приблизиться к дамочным полям. Впрочем, отыщите сами путь белых к выигрышу.

Белые: a1, е5. Черные: а5, с7. Ход белых.

Мы с вами расстаемся на то время, которое понадобится вам, чтобы отыскать решение.

Теперь сверьте свой ответ:

1. ef6 cd6 (1...ab4 2. fe7 bс3 3. ed8 ×) 2. fg7 de5 3. gf8! ef4 4. fh6 fg3 5. he3 ×. Все другие пути ложные и к победе не ведут.

Диаграмма 35. Ход белых

Очень важная позиция показана на диаграмме 35.

1. dc5 (здесь нельзя войти в соприкосновение с силами соперника, так как размен даст возможность черным занять оппозицию) 1... gf 6 2. cd6! (маневренность простой "f6" надо ограничить 2... hg5.

Что дальше? Идти в дамки? Рассмотрим такой вариант: 3. dc7 fe5 4. cd8 ed4 5. d:h4 dc3 6. hf6 cd2 7. fe3 d:f4 8. fd4. Победа! Но радость преждевременна. На четвертом ходу черные могут спастись, продолжая 4 ... ef4 5. d:h4 fg3 и т. д.

Оказывается, в дамки торопиться в этой ситуации не надо: 3. fe3!! gh4 4. dc7 hg3 5. ef4! g:e5 6. cd8 - самоограничение. Черные терпят поражение.

Для развития навыка расчета предлагаю решить следующие примеры.

№ 1. Белые: а3, g1. Черные: h2, f4.

№ 2. Белые: а5, e1. Черные: d6, g5.

№ 3. Белые: g1, g7. Черные: а3, g5.

Во всех позициях белые начинают и выигрывают.

Решения: № 1. 1. ab4 fe7 2. bс5 ef6 3. cd6! fg5 4. dc7 gf4 5. cb8 fe3 6. gf2 e:g1 7. ba7 ×.

№ 2. 1. ab6 gf4 2. ba7 fg3 3. ab8 gh2 4. b:g3! h:f4 5. ef2 ×.

№ 3. 1. gh8 gf4 2. hg7! (2. gf2 fe3 = ) 2 ... fe3 3. gh6 ef2 4. g:e3 ab2 5. hg7 - распутье.

Мы разобрали ряд примеров, где сильнейшая сторона остроумным путем одерживает победу. Но бывает, как вы уже знаете, что о выигрыше не может быть и речи. Больше того, позиции кажутся настолько безнадежными, что впору складывать оружие. Спасение в этом случае представляется настоящим чудом.

Вот примеры на эту тему:

Диаграмма 36. Ход белых

Диаграмма 36: 1. hg5 hg7 2. ef2! gh6 (2 ... hg1 3. gh6 = ) 3. fg3 = .

Диаграмма 37. Ход белых

Диаграмма 37: 1. de5! gh6 (1... ab6 2. ba5 ed6 3. e:c7= ) 2. ef6! e:g5 3. bc5. Белые проходят в дамки и занимают большую дорогу (три дамки выигрывают против одной только в том случае, когда они владеют большаком).

Диаграмма 38. Ход белых

Диаграмма 38: 1. ef4 bc5 2. hg5 cd4 3. gf6 dc3 4. fg5 h:f4 5. fg7 cd2 6. gf8 de5 7. fh6 fg3 8. hf4 = .

Диаграмма 39. Ход белых

Диаграмма 39: 1. eb4! ef2 (1... cb6 2. bc3 ba5 3. ce1 = ) 2. ba5 cd6 3. ab4 de5 4. bc3 ef4 5. cd2 fg3 6. del hg7 7. ec3 =

Диаграмма 40. Ход белых

Позиционная борьба приводит белых к поражению (см. диаграмму 40). Например: 1. cb4 bс5 ×; 1. gh2 bс5 2. fg3 fe3 3. gh4 ef2 4. hg5 fel! (не выигрывает 4... f g1 5. hg3! и ничего не дает 5... gd4 из-за 6. gf4) 5. gh6 e:b4 6. hg7 cd4 7. ef8 (единственный ход) 7... bа3 8. hg3 dc3 9. gh4 cb2 (можно и 9... ac1 10. fh6 cb2 11. hg5 ed4 ×) 10. hg5 bcl 11. gf6 (11. gh6 ce3 12. fg7 - иначе 13. ес5 × - 12... ed4 ×) 11... e:g7 12. f:h6 af8 × - столбняк на тройнике.

И все же спасение есть! Оно основано на "цугцванге", о котором мы рассказываем в следующей главе.

1. fg3 f:h2 2. cb4 ef4 (лучшего нет) 3. gf2!!, и выиграть черные не могут. Исключительно красивый прием!