
Глава IV. Условия, определяющие вероятность выигрыша и проигрыша
1. Первая степень наших познаний - есть предположение, которое обусловливает суждение. Вторая степень - убеждение, оно обусловливает надежду. Наконец, третья степень - уверенность или достоверность: она обусловливает познание.
Если бы все наши познания влекли за собой уверенность, то наши суждения обусловливали бы полное убеждение относительно известного предмета, и это убеждение должно было бы иметь решительное значение для всех. Но не так на самом деле: большая часть наших познаний есть простые вероятности, более или менее основательные, более или менее близкие к истине.
2. Достоверность имеет лишь одну степень, потому что она или есть, или ее нет; между тем как вероятность представляет собой бесконечное число степеней, потому что она может приближаться или удаляться от достоверности на столько, на сколько практическое суждение основывается на познаниях более или менее реальных. Следовательно, вероятность может измеряться, т. е. к ней приложены законы чисел.
Это приложение и составляет предмет теории вероятностей. Следовательно, это вычисление служит для сравнения различных гипотез, одних по отношению к будущим явлениям, других относительно причин уже известных явлений.
3. Факт, который неизбежно должен совершиться, называется достоверным.
Факт, осуществление которого зависит от наличности тех или иных причин, которые могут или благоприятствать, или препятствовать его возникновению, такой факт относится к области вероятных явлений.
Явление поэтому становится более или менее вероятным в зависимости от суммы благоприятствующих или препятствующих причин.
4. Для определения степени вероятности примем за единицу измерения понятие достоверности. Итак, достоверность = 1.
5. Вероятность определяется отношением числа причин, препятствующих возникновению явления, к числу причин, ему благоприятствующих. Отсюда формула вероятности может быть выражена геометрическим отношением.
Например, если 3 причины благоприятствуют возникновению явления, а 2 ему препятствуют, то вероятность возникновения явления выразится отношением 3/(2 + 3) = 5/3. Противоположная вероятность выразится в отношении 2/3; в означенной дроби числитель есть число причин, препятствующих возникновению явления, а знаменатель - число всех возможных причин.
Сумма этих дробей равняется единице, которая является выражением достоверности.
6. Вышеприведенные рассуждения формулируются в трех следующих теоремах Кондорсэ:
a) Если вероятность явления превышает 50%, что в применении к карточной игре формулируется 50 шансов, то явление скорее возникнет, чем не возникнет.
b) Ожидание выигрыша следует сопоставить со степенью вероятности, т. е. результат игры прямо пропорционален вероятности возникновения явления.
с) Указанные основания пропорциональны вероятности.
7. Шансы на выигрыш при данной вероятности выражаются произведением дроби, изображающей эту вероятность, на самую сумму.
Например, когда из пяти шансов игрок имеет три, чтобы выиграть сто франков, надежда его выразится произведением 100 франков на дробь 3/5, что будет равняться шестидесяти франкам.
8. Так как опасность проиграть есть противоположность надежде выиграть, то она (опасность) выразится произведением рискованной суммы на проигрыш. То, что называется выгода или невыгода (avantage ou desavantage) в игре, получается из комбинации надежд и опасностей игроков.
9. Если выигрыш какой-нибудь суммы подчинен появлению различных отдельных случайностей, то величина надежды, или судьба игрока, получается умножением раз личных благоприятных обстоятельств на стоимость суммы.
Когда надежде выиграть одно событие благоприятствует, а другое нет, то величина надежды выразится произведением благоприятной вероятности первого события на благоприятную вероятность второго, умноженным на стоимость суммы.
Все сказанное относится к простой вероятности какого-нибудь события.
10. Вероятность сложная вследствие совпадения не скольких событий равняется произведению вероятностей простых.
Это правило прилагается к появлению какого бы то ни было числа событий.
11. Задача I. Определить вероятность к выпадению грани одним очком, бросая два раза обыкновенную кость.
Так как кость имеет 6 граней, то вероятность, что грань с одним очком выпадет с первого удара, равняется 1/6; следовательно, 1/6 есть первая часть искомой вероятности.
Если грань с одним очком не выпала с первого удара, то она может выпасть со второго. Но так как вероятность, что 1 она не выпадет со второго удара равняется 1/6, а вероятность (по 9), что она выпадет со второго равняется 5/6 × 1/6 = 5/36, что составляет вторую часть искомой вероятности, то полная вероятность равняется 1/6 + 5/36 = 6/36 + 5/36.
12. Задача II. Определить вероятность выпадения грани с одним очком в три последовательных удара.
Вероятность выпадения этой грани с первого раза равняется 1/6. Если она не выпала с первого, то может выпасть с двух последующих. Следовательно, вероятность, что она не выпадете первого раза, равняется 5/6, а вероятность, что она не выпадет в следующих двух, равняется 5/6 + 11/36 = 55/216, что и составляет вторую часть искомой вероятности. Следовательно, эта вероятность будет 1/6 + 55/216 = 91/216.
Таким образом, по изложенному способу становится ясно, что вероятность выпадения грани с одним очком с четырех раз равняется 671/1296; с пяти = 3625/4151 и т. д.
Из этого видно, что вероятность увеличивается с числом выкидов кости и что возможно приблизиться как угодно близко к единице, или достоверности, увеличивая число опытов.
13. Примечание. Кто берется выбросить грань с одним очком в 4 раза, имеет столько же шансов, как и тот, кто берется двумя косточками выкинуть грани с шестью или семью в два удара, так как отношение вероятностей в обоих случаях равно 671:625.
По этому замечанию легко определить выигрыш игрока посредством шансов, которые он имеет перед противником, предполагая каждую ставку равной единице. Таким образом, мы находим, что выигрыш того, кто берется выбросить грани с одним очком в четыре раза, равняется
| 671-625 | = | 46 | , | ||
| 671+625 | 1296 |
или приблизительно 1/28 ставки своего противника.
14. Задача III. Определить вероятность 1/6 выпадения грани с одним очком два раза в два выкида.
Ясно (10), что вероятность будет равняться 1/6 × 1/6 = 1/36
15. Задача IV. Определить вероятность выбросить одною костью два раза грань с одним очком в три выкида.
Если в первый раз выпадет грань с одним очком, тогда дело будет заключаться лишь в том, чтобы другой as (грань с одним очком) выпал в два раза. Но так как вероятность, чтоб as выпал в первый раз, равняется 1/6, а вероятность, что он выпадет с двух (11), 11/36; то, следовательно, вероятность первого раза и вероятность второго равняется 1/6 × 11/36 = 11/216. Эта дробь есть первая часть искомой вероятности.
Если as не выпал с первого удара, то есть еще вероятность, что он выпадет с двух следующих ударов. Но так как вероятность, что он не выпадет с первого удара, равняется 5/6, а вероятность, что он выпадет в два следующих удара, равняется 1/36, то вероятность этих двух событий вместе = 5/6 + 1/36 = 31/216. Это есть вторая часть искомой вероятности. Следовательно, полная вероятность равняется 11/216 + 5/216 = 16/216. Точно так же вероятность, что выпадение двух as в четыре удара, равняется 171/1296.
16. Задача V. Определить шансы выпадения данного числа поэнов при выбрасывании известного числа костей с известным количеством сторон. Если, например, нужно узнать, сколько представляется шансов к выпадению поэна 16 при четырех костях, то увидим, что число искомых шансов = 125.
17. Все поэны, равно отстоящие как от самого малого, так и от самого большого числа поэнов, помещенных на костях, имеют одинаковое число шансов выпасть. Следовательно, если спрашивается, сколько шансов к выпадению поэна 16 при четырех костях, то, вычтя из 28, суммы двух крайних 24 и 4, в остатке получим 12, из чего можно заключить, что число шансов для поэна 16 есть то же, что и для поэна 12.
18. Задача VI. Определить вероятность выпадения грани с одним очком один раз в четыре удара.
Этот случай, в сравнении с возможностью выпадения поэна (12), наиболее редкий. Но так как первая часть вероятности равняется 671/1266, а вторая часть 171/1266, то из этого ясно видно, что искомая вероятность определяется следующим соотношением: 671/1296 - 171/1296 = 500/1296. Следовательно, шансы выпадения грани с одним очком один раз в четыре удара равняются отношению 500/796 = 5/8.
19. Задача VII. А и В играют вместе, у А не хватает только одного поэна, а у В двух. Спрашивается, какие у них относительные шансы выиграть партию.
Необходимо, чтобы партия окончилась по большей мере двумя поэнами.
Следовательно, ясно, что А может не выиграть один раз из двух, а В должен выиграть два раза кряду.
Допустив, что А и В имеют одинаковые шансы выиграть один поэн, вероятность, что В выиграет первый поэн, будет 1/2; следовательно, вероятность его выиграть два раза подряд будет 1/2 × 1/2 = 1/4. А потому возможность, которую имеет выиграть А один поэн из двух, будет 1 - 1/4 = 3/4, или относится как 3:1, следовательно, выгода будет в пользу А.
20. Задача VIII. А и В играют вместе; у А не хватает одного поэна и двух у В, но В имеет вдвое больше шансов, нежели А. Спрашивается, каковы относительные вероятности обоих.
B этой задаче, как и в предыдущей, видно, что В должен выиграть два поэна подряд. Но так как А имеет два шанса выиграть один поэн, а А имеет только один шанс, то вероятность, что В выиграет один, будет равняться 2/3; поэтому возможность его выиграть два поэна подряд будет 2/3 × 2/3 = 4/9.
Из этого видно, что вероятность для А выиграть партию будет 1 - 4/9 = 5/9 или будет относится как 5:4.
Из предшествующих задач видно, что когда у А не хватает только одного поэна для партии, а у В двух, то выгода в пользу первого будет относиться как 3:1.
Верность этих вычислений основана на известной игре - орлянка.
Игра эта состоит в бросании вверх монеты, у которой одна сторона называется орлом, а другая решеткой. Выигрывает тот, чья монета упадет орлом.
21. Задача IX. Спрашивается, каковы шансы, чтобы выпали орел или решетка два раза подряд.
Для этого существует четыре комбинации, а именно:
| Первый удар:{ | Орел | Второй удар:{ | Орел |
| Решетка | Орел | ||
| Орел | Решетка | ||
| Решетка | Решетка |
Из этих четырех комбинаций только в одну из них прорывает бросающий монету, следовательно, в его пользу три шанса вместо одного. Если бы дело шло о том, чтобы выпал орел или решетка в три удара, то было бы восемь комбинаций, из которых семь в его пользу, а одна нет; следовательно, шансы его выигрыша относились бы, как 7:1.
Но так как до начала игры вероятность, что выпадает орел с первого удара, равняется 1/2 и чтобы выпала сперва решетка, потом орел равняется 1/4, поэтому вероятность, чтобы орел выпал хоть раз в два удара, будет 1/2 × 1/4 = 1/8.
22. Задача X. Определить, во сколько опытов явление наверное произойдет.
Пример 1-й. Во сколько ударов, при одинаковых шансах, можно поручиться, что выпадет грань с двумя очками при двух костях?
Так как число различных ударов, которые могут выпасть при двух костях, равняется 36, между тем как есть только один шанс, что выпадет грань с двумя очками, то число противных шансов равняется 35. Умножая 35 на 0,7, мы получим произведение, которое покажет 24,5, что обозначает, что для получения желаемого результата необходимо от 24 до 25 ударов.
23. Пример второй. В лотерее, в которой число пустых и выигрывающих в отношении 39:1. Сколько нужно взять билетов, чтобы иметь одинаковые шансы получить один или несколько выигрышей?
Умножая 39 на 0,7, произведение укажет, что число искомых билетов будет 28,5, т. е. между 27 и 28.
Так же и в лотерее, в которой число пустых билетов будет относиться к числу билетов выигрывающих, как 5:1, произведение 3,5, полученное от умножения 5 на 0,7, показывает, что шансы более чем равны, если взять четыре билета; между тем как взявши три, они не будут представлять разности.
24. Примечание. В лотерее, в которой число билетов проигрывающих относится к числу билетов выигрывающих как 39:1, а всех билетов только 40, вышеозначенная пропорция была бы неуместна; потому что достаточно бы взять 20 билетов, чтобы можно было надеяться на выигрыш.
Кроме того, если всех билетов 80, сохраняя прежнюю пропорцию 39 пустых к 1 выигрывающему и, следовательно, предполагая 78 билетов проигрывающих и 2 выигрывающих, то и эта пропорция не будет годиться. Следовательно, если пропорция проигрывающих к выигрывающим часто будет повторяться, что обыкновенно и бывает в лотереях, то число билетов, которое нужно взять, чтобы выиграть, всегда будет равняться 0,7 отношения билетов проигрывающих к выигрывающим.
Шансы, или поэны, которые выпадают при двух или при большем количестве костей.
25. Очевидно, что при двух костях можно произвести тридцать шесть различных комбинаций, потому что каждая из шести сторон одной кости может быть последовательно шесть раз комбинирована с каждой из шести сторон другой. Поэтому при трех костях может быть 36*6 = 216 различных ударов, потому что тридцать шесть комбинаций двух костей могут быть комбинированы шесть раз с шестью сторонами третьей.
Поэтому можно держать 35 против 1, что не выпадет дублет, т. е. одинаковое число поэнов на одной и на другой кости (при двух костях).
Следующая таблица представляет все тридцать шесть комбинаций.
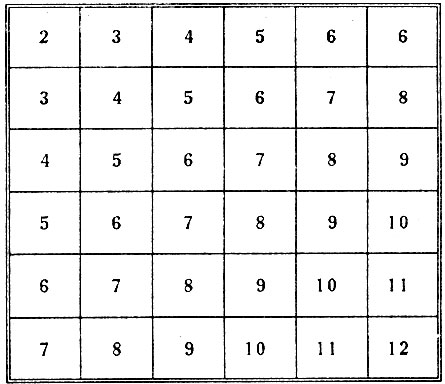
Тридцать шесть комбинаций
Предположим по первой вертикальной колонке этой таблицы, что одна из костей последовательно выпадает всеми ее сторонами, а другая только 1, во второй колонке, что на одной кости все выпадает 2, а остальная кость выпадает всеми своими сторонами и так далее. Одинаковые числа будут находиться на одной диагонали. Тут мы замечаем, что число 7 чаще всего выпадает при двух костях, между тем как всего реже выпадает 2 и 12.
Если таким образом устроить таблицу для трех костей, то получим шесть таблиц, в каждой по 36 чисел, и увидим, что 10 и М суть два числа, которые выгодней держать; что они выпадают при трех костях, так как благоприятные шансы от 27 до 216 относятся, или от 1 до 8; затем следуют числа 9 или 12; потом 8 и 13.
По этому способу можно определить самые вероятные числа, которые должны выпасть при данном количестве костей.
Необходимо знать различные комбинации известного числа костей, чтобы избежать невыгодных пари.
26. Если бросать две кости, как уже было замечено, вместе, то они образуют двадцать одно число; рассматривая их отдельно, они дают 26 различных комбинаций.
Из 21 удара, сделанного двумя костями, шесть первых называются дублетами и могут выпасть только одним образом, как, например: две шестерки, две четверки и т. д.
Остальные же 15 ударов представляют собою две комбинации, потому что на каждой из двух костей есть только по одной стороне 3 и 3 и два для 5 и 4, а именно: 5 же на первой кости и четыре на второй или четыре на первой кости, а пять на второй, так как таких случаев 36. Шансы, что выпадет данный дублет, будут относиться как 1:36; для неопределенного (indetermine) они будут относиться как 1:5 и как 1:17, чтобы выпало 6 и 4, тем более что это число имеет за себя два шанса против 24.
Слово (hasard) "случай" должно понимать в том смысле, какой придал ему г. Либри. Слово это будто бы происходит от арабского asar, что значит трудный, вследствие чего и итальянское выражение azari употребляется для названия чисел, которые труднее всего выбросить при трех костях.
27. При числе поэнов двух костей комбинация их шансов зависит от числа сторон, могущих произвести это число.
Если взяться выкинуть с первого удара число 11 двумя костями, то (hasard) шансы будут относиться как 2:34, для 7 шансы будут относиться как 6:30, так как 7 может выпадать шестью разными способами и иметь 30 неблагоприятных шансов. Нужно заметить, однако, что из тех 11 чисел, которые могут выпадать на двух костях, 7, число среднее между 2 и 12, имеет более шансов, нежели другие числа, которые со своей стороны имеют тем менее благоприятных шансов, чем ближе они лежат к крайним 2 и 12.
28. Чем больше число костей, тем значительнее увеличиваются шансы средних чисел в сравнении с крайними.
Если употреблять семь костей, крайние числа которых 7 и 42, а средние 24 и 25 и все к ним приближающиеся, как то: 22, 23, 26, 27. Если же вместо семи костей употреблять 25 и 150, можно почти ручаться, - что выпадет число 86 или 87.
Чтобы дать понятие о разорительной теории по лотерее, состоящей из семи костей, достаточно заметить, что шансы для выпадения vaftle относятся как 1:40.000, между тем как стоимость выигрыша не составляет и шестидесятой доли ставки.
Это-то и было причиною наживы игорных домов и лотерей.
То же самое можно сказать и о рулетке.
|
ПОИСК:
|
© TABLE-GAMES.RU, 2010-2020
При использовании материалов сайта активная ссылка обязательна:
http://table-games.ru/ 'Настольные игры'
При использовании материалов сайта активная ссылка обязательна:
http://table-games.ru/ 'Настольные игры'