Диалог пятый. ЭВМ и шахматные головоломки

- До сих пор наша беседа велась в довольно серьезном духе. Почему же теперь вдруг возник, судя по названию диалога, такой легкомысленный сюжет?

- Хотя темы, в самом деле, были серьезные, но чувства юмора мы не теряли, не правда ли?! Что же касается головоломок, то вы зря их недооцениваете. Во-первых, любителей математических развлечений не так мало, в часы досуга каждый любит поломать голову над какой-нибудь хитроумной задачкой. Так что вполне возможно, к этому диалогу, а заодно и к другим "прислушиваются" и люди, далекие от шахмат.

- Это вы неплохо придумали - таким способом расширить круг людей, увлекающихся и шахматами, и компьютерами.

- Надеюсь, это наша совместная цель. Но дело еще и в другом. Знаете ли вы, что именно головоломки привели к созданию многих важных разделов современной математики?

- Где-то читал об этом. Кажется, задача о кенигсбергских мостах, придуманная Л. Эйлером, лежит в основе одной классической задачи из теории графов.

- Можно сказать, что теория графов - важнейшая область прикладной математики - целиком произошла из головоломок. Кстати, вы помните, в чем суть задачи о кенигсбергских мостах?

- В общем, да. Некий остров омывается рекой с двумя рукавами и семью мостами. Надо выяснить, может ли пешеход обойти все мосты, пройдя по каждому из них по одному разу.

- Теперь вспомните, пожалуйста, не напоминает ли вам эта головоломка какую-нибудь шахматную.

- Да, она похожа на знаменитую задачу о коне, в которой этой самой загадочной шахматной фигуре требуется обойти всю доску, не останавливаясь ни на одном из полей дважды.

- Правильно. Между прочим, эта старинная задача о коне привлекла внимание великого математика Леонарда Эйлера. А другой великий математик Карл Гаусс интересовался еще одной занятной шахматной головоломкой: расставить на доске восемь ферзей так, чтобы никакие два из них не стояли на одной вертикали, горизонтали и диагонали, то есть не угрожали друг другу.

- Приятно, что выдающиеся ученые проявляли большой интерес к шахматам.

- Строго говоря, не к самим шахматам, а, можно сказать, к шахматной математике. Замечу, что обе головоломки, и о коне и о ферзях, содержатся в многочисленной литературе по теории графов и комбинаторике (еще одной области прикладной математики). В свое время эти задачи и подобные им побудили многих видных ученых заняться построением математического аппарата для их решения. В дальнейшем эта "математика" получила самостоятельное развитие, а сами задачи постоянно используются в научных изданиях в качестве иллюстраций и моделей различных математических понятий и проблем. Видите, как все сложилось и какое видное место отвоевали себе две эти шахматные головоломки?!

- Но какова роль компьютеров?

- Огромная! Точек соприкосновения между ЭВМ и головоломками более чем достаточно. Многие головоломки, в том числе шахматные, весьма сложны, и без помощи ЭВМ с ними не справиться. Не случайно некоторые необычные задачи придуманы в XIX веке, а решены только в XX!

Еще один важный аспект. Привлекая своим ярким содержанием, головоломки представляют собой прекрасные упражнения для тех, кто учится и совершенствуется в искусстве программирования. Здесь шахматам тоже повезло.

- А я все удивлялся, почему в книгах по программированию то и дело встречаются шахматные диаграммы, причем речь идет не об игре как таковой, а о различных расстановках фигур и их путешествиях по доске.

- Добавлю еще, что многие математические и компьютерные идеи удобно опробовать на головоломках.

- Наверное, вы имеете в виду ретроанализ, впервые примененный для решения шахматной головоломки? Может быть, с этого конкретного примера и начнем знакомство с головоломками?

- Я не против. Итак, задача о неприкосновенном короле (рис. 71). У белых на доске две фигуры - король, стоящий на поле c3, и ферзь на произвольном поле; у черных один король. Могут ли белые поставить мат, не делая ни одного хода своим королем?

Рис. 71

- По-моему, эта задача хотя и занимательна по форме, но относится, скорее, к серьезным шахматам.

- Многие из решавших ее, в том числе гроссмейстеры, полагали, что задание невыполнимо. Конечно, они не особенно утруждали себя и делали вывод из общих соображений. И тогда доктор физико-математических наук А. Брудно и кандидат физико-математических наук И. Ландау, также подозревая, что мата нет, решили убедиться в этом при помощи ЭВМ и составили программу ретроанализа.

- Но разве нельзя было обойтись обычным перебором, ведь на доске всего три фигуры, тем более одной из них запрещено двигаться?

- Давайте попробуем применить традиционный перебор "вперед". У белых всякий раз выбор примерно из 20 ходов, у черных- из пяти. Вариантов ход-ответ около 100. Всего вариантов просмотра на глубину 20 ходов (как мы скоро узнаем, меньшим числом в общем случае не обойтись) порядка 100²⁰ = 10⁴⁰. Если машина будет просматривать даже миллиард (10⁹) позиций в секунду, то анализ займет миллиарды лет...

- Если не ошибаюсь, возраст галактики меньше 100 миллиардов лет. Да, ждать придется чересчур долго...

- Теперь покажем, как упрощается дело, если за него взяться с умом. Заметим, что всего положений фигур не так много. Белый король прикован к полю c3, а в распоряжении белого ферзя и черного короля меньше 64 полей. Таким образом, общее число позиций не превосходит 64², то есть меньше 4000, с учетом очереди хода - 8000. Сведения о таком числе ситуаций легко поместить в память любого компьютера.

- "Эндшпиль", действительно, не отличается разнообразием позиций. Может быть, вы проиллюстрируете на нем идею алгоритма ранжирования?

- С удовольствием. Сейчас вы еще раз убедитесь в прозрачности метода ретроанализа.

Ранг выигранной позиции в данном случае - это наименьшее число ходов, за которое белый ферзь ставит мат. Сами матовые позиции образуют множество РЧо. Алгоритм состоит в том, что для каждого i = 0, 1, ... осуществляется следующая двухэтапная процедура:

1. Рассматриваются все неранжированные позиции с ходом белых. Если в какой-то из них у ферзя есть хоть один ход, ведущий в позицию из РЧ, то она получает ранг i + 1. Множество всех таких позиций - РБ_i+1.
2. Рассматриваются все неранжированные позиции с ходом черных. Если в какой-то из них любой ход черного короля ведет к уже ранжированной позиции (с ходом белых), то она также получает ранг i + 1 (получить меньший ранг она не может, так как тогда была бы ранжирована раньше).

Работа алгоритма заканчивается, когда при очередном значении i уже не возникает новых ранжированных позиций.

- Действительно, все понятно. Каков же результат исследования головоломки на ЭВМ?

- Она исследовалась на компьютере при всех положениях неприкосновенного короля, и в результате выяснилось, что белые достигают цели только при его положении на c3 или на симметричных полях c6, f3 и f6. При этом максимальный ранг L равен 23, то есть мат дается не позднее 23-го хода при любом начальном положении белого ферзя и черного короля.

Данный пример примечателен тем, что впервые в истории ЭВМ решила шахматную задачу раньше человека!

- Неужели никто из ваших знакомых не смог самостоятельно справиться с этой головоломкой?

- Теперь я могу признаться, что если квалифицированному шахматисту сообщить, что мат есть, то он его в конце концов находит. Хотя часик-другой задачка у него отнимет.

- Тогда я сразу сдаюсь и прошу вас показать решение.

- Прежде всего необходимо загнать черного короля на угловое поле a8. С этим заданием ферзь легко справляется, занимая при этом поле d7. На приведенной выше диаграмме изображена как раз такая ситуация. Если теперь ход черных, то белые матуют в 10 ходов: 1... Kpb8 2. Фe6 Kpa7 3. Фc8! Kpb66 4. Фc17! Kpc5 (4... Kpa6 5. Фb7 и 4... Kpa6 5. Фc7 Kpb5 6. Фd6 ведет к основному варианту) 5. Фe6 Kpb5 6. Фd6 Kpa5 7. Фb4+ Kpa6 8. Фb8 Kpa5 9. Фb7 Kpa4 10. Фa6×.

- Ну а если ход белых, то они должны передать его очередь противнику: 1. Фd5+ Kpa7 (1... Kpb8 2. Фe6!) 2. Фb5 Kpa8 3. Фa6+ Kpb8 4. Фe6! и цель достигнута. Это напоминает популярный в теории окончаний метод треугольника. Я прав?

- Как шахматист вы абсолютно правы.

- А как кто я не прав?

- Как компьютер! При матовании машина сумела сэкономить целый ход! Кстати, вы не догадываетесь, какая позиция рекордная?

- Наверное, когда короли удалены друг от друга на максимальное расстояние. Поскольку белый неприкосновенен, то черный должен располагаться на h8.

- Теперь вы правы и с точки зрения компьютера... Чтобы сохранить симметрию на доске, поставим белого ферзя на a1 (рис. 72). Вот как он объявляет мат в 23 хода.

Рис. 72

1. Фd5 + Kpg7 2. Фb5 Kpg8 3. Фb6 Kpf7 4. Фg5 Kpf8 5. Фg6 Kpe7.

- Я, кажется, сообразил, каким образом ферзь увлекает черного короля в опасную зону: 6. Фf5 Kpe8 7. Фf6 Kpd7 8. Фe5 Kpd8 9. Фe6 Kpc7 10. Фd5 Kpc8 11. Фd6 Kpb7 12. Фc5.

- Пока все четко. Между прочим, такой прием циклического повторения маневров группы фигур, в данном случае двух, в шахматной композиции называют систематическим движением. Сейчас наступил важный момент: на естественное 12... Kpb8 следует 13. Фe6 и, как мы знаем, мат дается через восемь ходов, а всего понадобится 22.

- Значит, черные должны играть 12... Kpa8, затягивая сопротивление.

- Теперь согласно рекомендованному вами методу треугольника следует продолжать 13. Фd5 Kpa7 14. Фb5 и т. д. Но тогда решение займет 24 хода - это не устраивает белых.

13. Фb5! Вот где экономится темп: машина сделала этот ход сразу. 13... Kpa7 14. Фd5! Kpb8 (a6) 15. Фe6 (+) Kpa7.

- И перед нами знакомая позиция, которая получается в указанном вами решении после второго хода. Впереди их еще восемь. Складываем и получаем 15 + 8 = 23, что и требовалось доказать!

- Осталось заметить, что идея ретроанализа применяется при решении различных переборных задач, но ее шахматная иллюстрация, пожалуй, наиболее наглядна.

- Задача о неприкосновенном короле - это нечто среднее между головоломкой и шахматным окончанием. Теперь, наверное, стоит сосредоточить внимание на чистых головоломках, чтобы наш диалог соответствовал своему назначению...

- Компьютер умеет решать самые разнообразные шахматные головоломки. Мы остановимся на тех, которые связаны с наиболее популярными шахматными персонажами,- ферзем и конем. Какая из этих фигур вам милее?

- Ферзь все-таки сильнее коня!

- Значит, начнем с задачи о расстановке ферзей, встречающейся, между прочим, и в популярной, и в научной литературе. Например, много внимания уделено ей в книге А. Брудно и Л. Каплана "Олимпиады по программированию для школьников".

- Там тоже есть шахматный материал?

- И довольно интересный! Несколько слов о "происхождении" этой книги. В 1972 году в Октябрьском районе Москвы был открыт Учебно-производственный центр вычислительной техники на базе Института электронных управляющих машин.

- Кто занимается в центре?

- Ученики старших классов близлежащих школ района. Около половины из них специализируются по программированию и получают квалификацию программиста-лаборанта.

- Жаль, что я уже кончаю школу! Не отказался бы повысить свою компьютерскую квалификацию!

- Начиная с 1980-го раз в году в центре проводятся Московские городские олимпиады по программированию с участием учеников центра и всех желающих. В книге А. Брудно и Л. Каплана как раз и приведены все задачи первых пяти олимпиад, алгоритмы их решения и программы для ЭВМ на Алголе и Фортране. А в двух параграфах книги исследуются темы, связанные с задачами на большой перебор. И посвящены они... шахматам.

- Что же это за темы?

- Одна о ретроанализе применительно к задаче о неприкосновенном короле - об этом шла речь выше, другая о задаче о расстановке ферзей!

- Может быть, вы немного расскажете об истории этой задачи?

- С удовольствием. Прежде всего уточню ее формулировку. Итак, задача о восьми ферзях. На шахматной доске требуется расставить восемь ферзей так, чтобы они не угрожали друг другу, кроме того, надо подсчитать, сколькими способами это можно сделать.

- Наверное, особенно трудна вторая часть задачи.

- Конечно, найти одну расстановку сумеет каждый.

- Вы говорили, что задачей о ферзях увлекался великий Гаусс.

- Да, в середине прошлого века он действительно интересовался головоломкой, но, как ни странно, всех решений не нашел!

- Неужели такое возможно?

- Представьте себе, он обнаружил только 72 решения. И лишь в 1874 году было строго доказано, что общее число искомых расстановок равно 92.

- Забавно, что когда-то этот подсчет мог вызвать такие сложности. В наше время полный набор расстановок машина представит за считанные секунды.

- Но перед тем как написать программу, надо составить хороший алгоритм. Этот диалог, между прочим, я и затеял с целью подробно описать какой-нибудь переборный алгоритм. Конечно, головоломка с ферзями не шахматная игра, а некий математический вопрос. Достоинство задачи в том, что алгоритм ее решения удается изложить в компактной форме. Кстати, как бы вы приступили к поиску необходимых расстановок?

- Я бы воспользовался тем, что на каждой вертикали, горизонтали и диагонали разрешается стоять только одному ферзю. Первого я поставил бы на любое поле вертикали "a"; второго - на одно из полей вертикали "b", но чтобы он не напал на первого; третьего - на вертикаль "c" и чтобы ему не угрожали первые два и т. д. Так продолжал бы до тех пор, пока восьмой, Последний ферзь не занял свое законное место на вертикали "h". Вот и получил бы одну из искомых расстановок.

- Не все так просто. Ведь в этом поиске вполне может случиться, что для очередного ферзя не найдется места на следующей вертикали. Как вы тогда будете выкручиваться?

- Сделаю шаг назад, переставлю ферзя предыдущей вертикали на другое подходящее поле и снова двинусь вперед.

- А если ни одна из попыток не увенчается успехом?

- Отступлю еще на одну вертикаль назад, а потом снова двинусь вперед.

- В целом идея правильная. А найдя одну из расстановок восьми ферзей, как будете искать следующую?

- Использую только что найденную. Сниму восьмого ферзя с вертикали "h", а для седьмого постараюсь найти новое поле на вертикали "g". Дальше в зависимости от обстоятельств двинусь вперед или назад уже по знакомой схеме. Конечно, иногда придется переставлять и самого первого ферзя на вертикали "a". Поменяв его место, вновь начну движение вперед.

- В конце концов возникает ситуация, когда вы не сумеете найти ни одной новой расстановки.

- Значит, работа алгоритма закончена: все необходимые решения получены, попутно подсчитано и их число. Но я должен вам прямо заявить, что все это делать вручную не собираюсь! Время слишком дорого.

- Не волнуйтесь, за вас постарается компьютер. Но разрешите придать вашим рассуждениям более математический вид.

- Мне и самому это интересно.

- Заметьте, что в вашем алгоритме предусмотрены как бы три вида движения.

- Какие именно?

- "Вперед" - когда закреплен i-й ферзь и вы переходите к поиску места для (i + 1)-го; "вбок" - в процессе нахождения места для этого (i + 1)-го ферзя; наконец, "назад" - если поставить (i + 1)-го ферзя не удалось и надо менять место i-го.

- И что нам дает это уточнение?

- Как вы знаете, одной из самых удобных и наглядных форм задания алгоритма является блок-схема - иллюстрация в виде отдельных, элементарных шагов. Четкое описание операций "движения" позволяет построить подробную блок-схему алгоритма для задачи о восьми ферзях. Обозначим через i номер очередной вертикали в алгоритме, а через j номер горизонтали для ферзя, занимающего i-ю вертикаль (i, j = 1, 2, ..., 8).

- Вы знаете, я внимательно рассмотрел блок-схему на рисунке 73 и убедился, что по ней действительно легко разобраться в работе алгоритма.

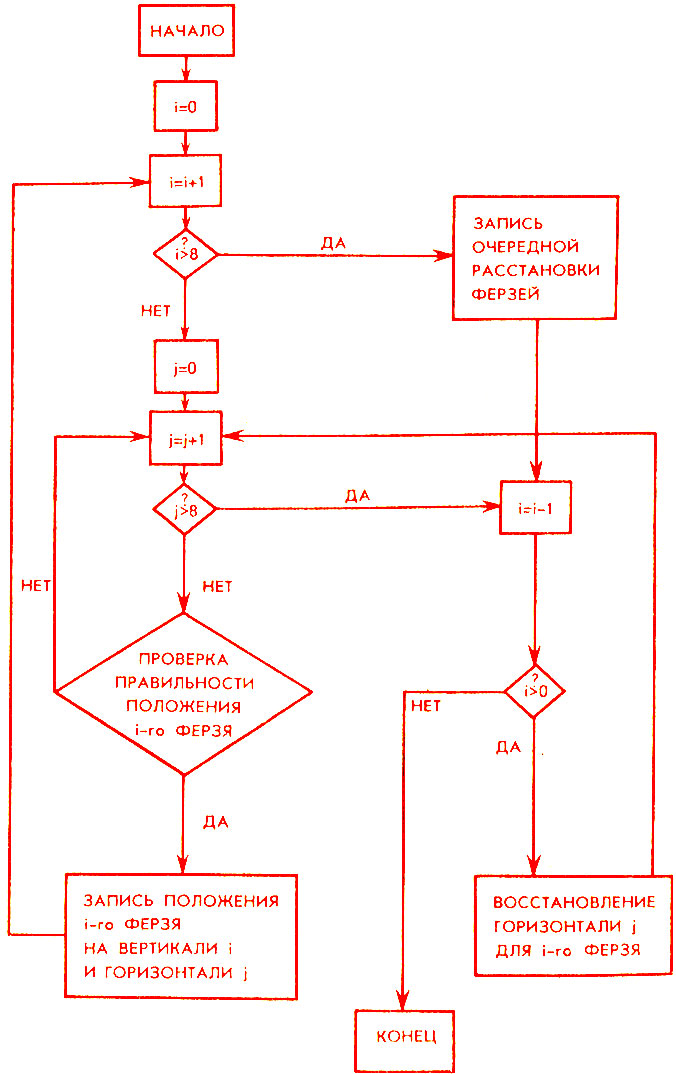
Рис. 73. Блок-схема алгоритма решения задачи о восьми ферзях

- Тому, кто пожелает узнать, как она превращается в конкретную машинную программу, советую заглянуть в упомянутую выше книгу про олимпиады по программированию. В ней, кстати, приведено пять различных алгоритмов и соответствующих программ решения задачи, причем каждый последующий вариант улучшает предыдущий по скорости нахождения расстановок.

- За счет чего это происходит?

- Упомяну простейший способ "усиления" алгоритма. При фиксировании места для очередного ферзя следует запоминать номера горизонтали и диагонали, на которые он попал. Тогда при движении "вперед" ставить ферзей на эти линии уже не надо, и алгоритм работает быстрее.

- Может быть, стоит привести здесь все 92 расстановки ферзей, не угрожающих друг другу? Если кто-нибудь попробует написать программу самостоятельно, то он сможет проверить ее правильность.

- Между прочим, достаточно ограничиться двенадцатью расстановками вместо

- Что это за особые экземпляры?

- Это произвольный набор расстановок, обладающий двумя свойствами:

1. ни одна из них не переходит в другую из того же набора при поворотах и зеркальных отражениях доски;
2. любая искомая расстановка восьми ферзей либо входит в набор, либо получается из какой-нибудь расстановки набора при помощи этих преобразований доски.

- И доказано, что всякий такой набор содержит ровно 12 расстановок?

- Да, причем математически строго. Вот один из наборов, обладающий двумя замечательными свойствами:

1. Расстановка на рисунке 74.
   
   Рис. 74
   
   
2. Расстановка на рисунке 75.
   
   Рис. 75
   
   
3. a4, b1, c5, d8, e6, f3, g7, h2.
4. a4, b2, c5, d8, e6, f1, g3, h7.
5. a4, b2, c7, d3, e6, f8, g1, h5.
6. a4, b2, c7, d3, e6, f8, g5, h1.
7. a3, b5, c2, d8, e6, f4, g7, h1.
8. a4, b1, c5, d8, e2, f7, g3, h6.
9. a4, b7, c3, d8, e2, f5, g1, h6.
10. a6, b4, c2, d8, e5, f7, g1, h3.
11. a4, b8, c1, d5, e7, f2, g6, h3.
12. a4, b2, c7, d5, e1, f8, g6, h3.

Остальные 80 расстановок получаются из этих двенадцати при помощи поворотов и зеркальных отражений доски. Первая расстановка дает всего четыре решения, а другие 11 - восемь. Итого, 1×4 + 11×8 = 92 расстановки восьми ферзей, не угрожающих друг другу.

- Чем привлекла задача о восьми ферзях Гаусса?

- Он обнаружил тесную связь между этой шахматной головоломкой и одной чисто арифметической задачей. Если вам это интересно, рекомендую полистать мою книжку "Шахматы и математика".

- А кто-нибудь пытался обобщить задачу о восьми ферзях для других досок?

- Наиболее интересное сообщение связано с переходом к доскам пХп. Математически доказано, что при любом п (отличном от 2 и 3) наибольшее число ферзей, не угрожающих друг другу на доске пХп, равно п.

- И можно приспособить наш алгоритм для поиска всех решений?

- Нет ничего проще! Для этого в нашей блок-схеме достаточно в "счетчиках" для i и j число 8 заменить на соответствующее значение n (то есть в двух ромбовидных фигурах слева поставить i>n и j>n). Правда, с увеличением n объем вычислений катастрофически растет. Кстати, при помощи ЭВМ найдено число расстановок n "мирных" ферзей для всех n≤15. Цифры получаются "миллионные", а для больших значений п задача вообще не решалась.

- Все время хочу спросить: а почему А. Брудно на занятиях по программированию пользовался именно задачей о ферзях?

- Между прочим, с этим вопросом я тоже обратился к Александру Львовичу. Он ответил мне в письменной форме:

"Перебор вариантов является сердцевиной программ искусственного интеллекта независимо от того, к чему он прилагается - исследованию игр, выбору решений, распознаванию образов и т. д.

Между тем даже опытный программист, знающий операционные системы и языки программирования, зачастую оказывается беспомощен в программировании задач перебора, поскольку его схема не укладывается в традиционные схемы циклов. Действительно, особенность сложного перебора, заключающаяся в постоянном движении вперед и назад, не подходит под стандартный цикл - однократный по i или двукратный по i и j,- встречающийся при написании обычных алгоритмов и программ.

Алгоритм решения задачи о ферзях достаточно общий, он пригоден для самых разных случаев перебора. Однако для детального объяснения работы алгоритма и программы на ЭВМ я не сумел найти лучшего примера, чем шахматная головоломка! С одной стороны, она включает в себя все возможные нюансы, а с другой - весьма интересна и понятна школьникам".

В завершение ферзевой темы рассмотрим одну необычную игру, в которой машина сумела досконально разобраться без участия человека.

- Это какая-то фантастическая шахматная игра?

- Скорее, это игра математическая. Двое игроков ставят по очереди ферзей последовательно на вертикали "a", "b", "c" и т. д. Никакие два из них не должны нападать друг на друга.

Проигрывает тот, кто не может сделать очередного хода.

- Приведите, пожалуйста, какую-нибудь иллюстрацию.

- Вот две короткие партии.

Рис. 76

- В первом случае (рис. 76) белые (начинающий) выиграли в 5 ходов: все поля вертикали "f" под контролем, а во втором (рис. 77) - в 4 хода выиграли черные: на вертикали "e" не осталось ни одного доступного поля. Кстати, вторая партия рекордно короткая.

Рис. 77

- В самом деле, при любой расстановке трех ферзей (не угрожающих друг другу) на вертикалях "a", "b" и "c" на следующей вертикали всегда найдется поле еще для одного ферзя.

- Интересен и другой вариант игры: тот, кто делает ход последним, выигрывает столько очков, сколько свободных вертикалей еще осталось на доске.

- При таком правиле в первом примере белые выиграли 3 очка, а во втором черные - 4.

- Возникает вопрос: в чью пользу игра в ферзей в каждом из двух вариантов?

- Наверное, можно перебрать все возможные партии. Мне кажется, их не так много.

- Вы правы, легко убедиться, что число партий не превышает нескольких тысяч. Но все же заниматься перебором вручную довольно скучно, и эта работа была полностью доверена компьютеру.

- И что же оказалось?

- Машина сделала следующие выводы. В первом варианте у черных имеется выигрывающая стратегия. А во втором варианте при наилучших действиях обеих сторон партия заканчивается вничью - выигрыш игрока, поставившего последнего ферзя, составляет 0 очков!

- Я немного знаком с математической теорией игр, и в ее терминах это означает, что цена игры равна 0.

- Так и есть... А мы можем сделать вывод, что во втором варианте игра длится восемь ходов и каждый ставит на доску по 4 ферзя. На рисунке 78 один из примеров ничейной партии.

Рис. 78

А сколько, на ваш взгляд, всего существует партий?

- Ну, знаете, моей сообразительности вполне хватает, чтобы установить связь между этой игрой и задачей о ферзях. Поскольку между "мирными" расстановками восьми ферзей и ничейными партиями (во втором варианте игры) существует взаимно однозначное соответствие, то всего партнеры могут разыграть 92 партии с ничейным исходом!

- Каков алгоритм игры?

- Нужно действовать довольно тонко: на каждом ходу следить за тем, чтобы уже поставленные ферзи можно было дополнить хотя бы одним способом до какого-нибудь решения головоломки.

- Согласитесь, что без предварительного анализа, проведенного компьютером, нелегко было бы догадаться, чем завершится игра в ферзей.

- Без компьютера нам никуда не деться!

- Перейдем к другой популярной головоломке, которую называют задачей о ходе коня. Помните, в чем она заключается?

- Требуется обойти конем все поля шахматной доски, причем так, чтобы каждое из них посетить по одному разу.

- Особая популярность задачи объясняется тем, что в XVIII и XIX веках ею занимались многие крупные математики, а Эйлер посвятил ей большой мемуар "Решение одного любопытного вопроса, который, кажется, не поддается никакому систематическому исследованию".

- Название этого математического труда, надо сказать, несколько легкомысленное...

- Но ведь и тема не слишком серьезная для знаменитого математика.

- Эйлер придумал эту задачу?

- Нет, но он первым обратил внимание на ее математическую сущность. Кстати, проблема не в том, чтобы найти какой-то определенный маршрут коня, а в подсчете всех возможных путешествий коня по доске.

- В конце концов с этой проблемой удалось справиться?

- Увы, нет. Задача не решена до сих пор, и, похоже, нам не в состоянии помочь никакой компьютер. Известно, правда, что число решений не превосходит C₁₆₈⁶³ (число сочетаний из 168 элементов по 63, оно состоит из ста цифр), но больше 30 миллионов. Математик Ф. Миндинг, подошедший к проблеме с алгебраической точки зрения, предложил метод, позволяющий вывести формулу для числа всех решений, однако вычисления, которые следует при этом произвести, практически неосуществимы.

- Но я читал, что для нахождения различных маршрутов коня придумана масса способов.

- Да, и каждый из них порождает целое множество решений. Так что, по сути, мы имеем дело с тем или иным алгоритмом. Вот некоторые известные методы: Эйлера и Вандермонда, рамочный метод Мунка и Коллини, метод деления на четверти Полиньяка и Роже, "раздельный ход коня", магический квадрат и др.

- Названия звучат довольно загадочно. А какой алгоритм проще всего для конкретного поиска маршрута?

- Удобнее всего пользоваться правилом Варнсдорфа:

1. при обходе доски коня следует всякий раз ставить на поле, с которого он может сделать наименьшее число ходов на еще не пройденные поля;
2. если таких полей несколько, то можно выбирать любое из них.

- Но является ли это правило алгоритмом, ведь его вторая часть сформулирована не очень четко?

- Тонкое замечание! В принципе эту часть правила легко уточнить так, чтобы очередное поле маршрута определялось однозначно. Вот здесь как раз и постаралась машина.

- По-моему, метод настолько прост, что человек может обойтись без электронных помощников.

- Напомню, что правило Варнсдорфа было предложено более 150 лет назад и долгое время считалось совершенно безукоризненным. Но вот машинный эксперимент, проведенный под руководством А. Есаяна, показал, что произвольное применение второй части правила может привести коня в тупик.

- Ввиду неудачного старта коня в его далеком путешествии?

- В том-то и дело, что это не имеет значения. Машина доказала, что, с какого бы поля конь ни начал свое движение, существует путь, который удовлетворяет правилу Варнсдорфа, но при этом обрывается раньше полного обхода доски.

- Требуется пример...

- Пожалуйста. Занумеруем последовательно поля, которые посещает конь (рис. 79).

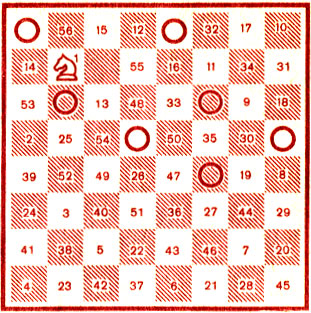
Рис. 79

Здесь видно, что, начав маршрут с поля b7, конь сделал 55 ходов, дошел до b8, а дальше двинуться не может. Увы, он вынужден был встать на поле с номером 56, поскольку с него имеется наименьшее число дальнейших перемещений, а именно 0. В результате восемь полей (a8, b6, c7, d5, e8, f4, f6, h5) остались непройденными - они помечены кружками.

- Да, плохо дело. Получается, что машина в данном случае сыграла негативную роль для классической задачи о ходе коня.

- Отрицательный результат тоже результат! Но не надо огорчаться. Машина проявила себя вполне достойно.

- Что вы хотите этим сказать?

- Известны примеры, когда компьютер справлялся с задачей, не поддающейся человеку,- я имею в виду не только шахматные программы: не раз машина доказывала, что та или иная задача не имеет решения и все его поиски напрасны. Однако данная находка компьютера иного рода! Здесь нет особых опровержений и доказательств, но зато машина внесла полную ясность в этот старинный метод решения задачи о коне.

- Значит, все-таки правило Варнсдорфа оправдывает себя?

- Вполне, но требует некоторого внимания. Машина доказала и другой факт: с какого бы поля конь ни начал свое движение, существует путь, который удовлетворяет правилу Варнсдорфа, но приводит к обходу всей доски.

- На первый взгляд два сделанных утверждения противоречат друг другу.

- Ни в коем случае. Просто компьютер выяснил для себя и для нас тоже, что второй частью правила Варнсдорфа надо пользоваться аккуратно. Произвольное обращение, как мы видели, может привести к неприятностям.

- На этом примере мы убедились в справедливости первой теоремы. Хотелось бы на нем же увидеть, что верна и вторая.

- Пожалуйста. Неточен был 51-й ход Kd3-b4. С поля 52 у коня две возможности - на a6 и d5, но столь же немногочисленный выбор у коня и с поля f4 (на d5 и h5). Его-то и надо было предпочесть. Теперь коню легко завершить необходимый маршрут: Kf4-h5-f6-e8-c7-a8-b6-d5. Итак, на всех полях с кружочками конь побывал. Еще нужно не забыть обойти ряд полей старого маршрута, с 52-го по 56-й: Kd5-b4-a6-b8-d7-c5, и на доске не осталось ни одного поля, которое бы не посетил конь, причем ровно один раз!

Заметьте, что мы получили своеобразный маршрут коня, называемый замкнутым: с конечного пункта путешествия - c5 конь может прыгнуть на исходный - b7.

- Уточнение маршрута нашла машина?

- Честно говоря, я это сделал сам. Но понятно, что для машины это не работа...

- А что еще интересного можно ожидать от компьютера, решающего задачу о ходе коня?

- Он может строить занятные графики, которые получаются в результате последовательного соединения прямолинейными отрезками центров полей, посещаемых конем.

- Эти графики могут иметь необычный вид?

- Иногда они довольно забавны. Вот два достопримечательных примера такого рода.

Рис. 80

График первого маршрута (рис. 80) - он "замкнут" - напоминает собой вазу, а график второго (рис. 81) - он "открыт" - подобен цветку, части которого расположены в высшей степени симметрично. Если поэкспериментировать на компьютере, то, думаю, можно получить и другие занятные картинки...

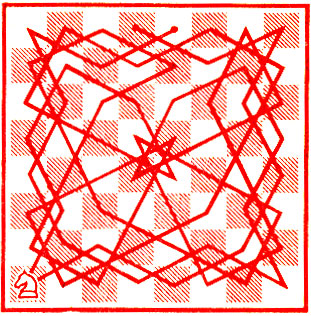
Рис. 81

- Графическое изображение маршрутов коня, видимо, имеет лишь эстетическую ценность.

- Не совсем так. В этой области тоже придуманы любопытные головоломки, для решения которых без компьютера не обойтись. Обратите внимание: оба наших маршрута самопересекающиеся, причем точек самопересечения немало!

- Неужели конь может обойти всю доску по маршруту, график которого не имеет самопересечений?

- Ну, на это рассчитывать не приходится. Собственно, задача так и ставится: на шахматной доске найти самый длинный, то есть содержащий наибольшее число ходов, несамопересекающийся путь коня. Вы возьметесь установить рекорд?

- Я могу попробовать нарисовать картинки. Но, найдя какой-нибудь график, как я докажу, что он самый длинный?! Подозреваю, что рекорд установил компьютер...

Рис. 82

- Вы угадали, даже сразу два! Искомый путь коня (рис. 82) состоит из 35 ходов, и независимо друг от друга его нашли сразу две ЭВМ - американская и западногерманская.

- Да, весьма извилистый путь. Вот если бы доска была чуть меньше, я бы тоже сделал попытку посостязаться с машиной.

- Боюсь, что вы проиграли бы эту "партию". Задача была исследована для всех досок со стороной не больше десяти клеток, и что вы думаете: ни один человек из решавших задачу не сумел найти на доске 6×6 путь, содержащий более 16 ходов. Рекорд установил компьютер!

На рисунке 83 самый длинный несамопересекающийся путь, предложенный машиной: он содержит 17 ходов!

Рис. 83

- Сознаюсь, я никак не ожидал, что наш заключительный диалог пройдет столь увлекательно. В самом деле, в области шахматных головоломок успехи ЭВМ просто удивительны. Но вот что меня смущает: не слишком ли специфичен этот материал, все-таки практиков он может не заинтересовать.

- Я всегда был уверен, что шахматисты любят решать необычные задачи. Ведь и шахматы - это, по существу, головоломка, хотя и очень сложная. Но если вы считаете разумным привести головоломку с более "практическим" содержанием, то у меня в запасе есть и такая. Небольшая новелла, которая завершит наши диалоги, называется "Охота на мустанга".

В вычислительном центре Воронежского университета еще в 70-е годы проводились исследования по сравнительной эффективности различных алгоритмов анализа конфликтных ситуаций. Примечательно, что при этом в качестве моделей использовались игры, одна из них - борьба ладьи против коня (короли отсутствуют!). В исследовании этой игры компьютер добился блестящих результатов.

- Ясно, что "сражение" протекает при территориальном преимуществе ладьи, и вопрос лишь в том, сможет ли она поймать коня.

- Этим и объясняется название игры - "Охота на мустанга".

- Думаю, что традиционная доска малоинтересна: поймать на ней коня вряд ли возможно, если не считать некоторых особо неудачных ситуаций, когда он ловится немедленно.

- Но при уменьшении размеров доски положение коня становится все более опасным. На доске 8×5 большинство начальных позиций еще ничейно, а вот на доске 8×4 ладья уже легко ловит кoня при любом начальном положении фигур (рис. 84).

Рис. 84

1. Лc3! Kd1 (1... Kh1 и 1... Kg4 сразу проигрывают ввиду 2. Лf3) 2. Лc2! Ke3 3. Лd2 Kf1 (3... Kc4 4. Лe3 Kb2 5. Лd4!) 4. Лe2 Kg3 5. Лe1! - конь пойман, и следующим ходом ладья уничтожает его. Другой вариант: 1... Ke4 2. Лf3! Kd2 3. Лe3!, и после 3... Kf1 или 3... Kc4 дело сводится к предыдущему.

- Обратимся к позиции на рисунке 84. Можете сразу сдаться.

- Вы правы: не знаю, сумею ли я поймать здесь коня.

- Между прочим, до того как А. Левин и О. Ускова предложили эту позицию ЭВМ, они были совершенно уверены, что на такой доске поймать коня невозможно. Машина опровергла эту гипотезу, установив, что ладья всегда ловит коня.

1. Лd4! Kc3 (быстрее проигрывает 1... Ke3 2. Лd2 или 1... Kb6 2. Лd2 Ka4 3. Лc2 и далее Лc5-c4-d4). 2. Лd2! Ke4 3. Лe3. Если сейчас 3... Kc5, то 4. Лd4 и на 4... Kb3 - следует маршрут 5. Лc4! Kd2 6. Лb4! Kf 1 (f3) 7. Лe4! Kd2 8. Лe3! На 3... Kf2 решает 4. Лe3 Kd1 5. Лf3 Kb2 6. Лc3 Kdl (6... Ka4 7. Лc4 и 8. Лd4) 7. Лc2 Ke3 8. Лd2 Kf1 9. Ле2 Kg3 10. Лe1. Важно отметить, что при любом другом ходе ладьи выигрыша уже нет, хотя мустангу и предстоят опасные гонки! Вот один из вариантов: 1. Лс4? Ke3! 2. Лf4 Kc2! (2... Kd5? 3. Лd4, 2... Kd1! 3. Лf3) 3. Лe4 Ka3! 4. Лe2 Kb5! (4... Kc4? 5. Лc2 Kd6 6. Лc3) 5. Лd2 Kc3!, и белые в цугцванге: 6. Лd4 Ke2 7. Лc4 (7. Лd3 Kf4!) 7... Kg1 (7... Kg3? 8. Лc2 Ke4 9. Лe2 и 10. Лd2) 8. Ле4 Kf3! 9. Лg4 Kel! (9... Kd2? 10. Лf4 Kb3 11. Лc4) с ничьей.

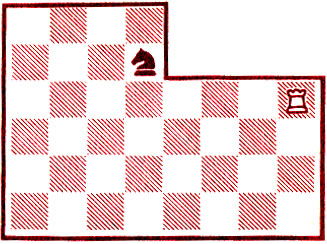
Рис. 85

Вы убедились, какая напряженная борьба возможна при столь мизерном материале?

- Да, поистине в рассмотренном жанре компьютер оказался "на коне"!

Вспоминая содержание наших диалогов, я все больше убеждаюсь, что компьютерам под силу все! И в шахматной игре, и в анализе эндшпиля, и в решении головоломок их достижения весьма велики. Я, конечно, уважаю прогресс, и ИТР меня вдохновляет, и все же немного обидно становится за человека...

- К концу наших бесед вы, кажется, впали в сентиментальность. Не отчаивайтесь: до сильнейших гроссмейстеров компьютерам далеко, анализировать они умеют лишь определенные классы эндшпиля, да и в решении головоломок, если те содержат изюминку, человек перехитрит любую машину. В качестве иллюстрации обратимся к замечательному примеру, придуманному американским математиком С. Нортоном (рис. 86).

Рис. 86

- Это уже обычная шахматная позиция?

- Не совсем: на доске два короля и ладья, но сама доска нестандартная - она не ограничена с двух сторон. Поэтому на диаграмме и отрезаны верхняя и правая границы. Вопрос состоит в том, могут ли белые заматовать неприятельского короля при данном положении фигур. Вы как считаете?

- На первый взгляд задание невыполнимо, поскольку черный король убегает на север или восток. А если ладья мешает ему, то король приближается к ней, сгоняет с места, и одно из двух направлений освобождается.

- Любопытно, что многие шахматисты, которым предлагалась эта задача, также были уверены, что мат поставить нельзя. Однако белые добиваются цели, хотя, как ни странно, рамок обычной доски им для этого не хватает!

Очевидно, компьютер, способный в привычных условиях, как мы знаем, поставить слабейшей стороне мат не позднее 16-го хода, в данном случае бессилен - ему просто в голову не придет перемещать фигуры вне квадрата 8×8. Традиционный алгоритм матования и программа для ЭВМ здесь непригодны. Скажу вам, что при данном положении фигур, кстати самом неудачном для белых, они ставят мат, не выпуская черного короля за пределы прямоугольника 9×11.

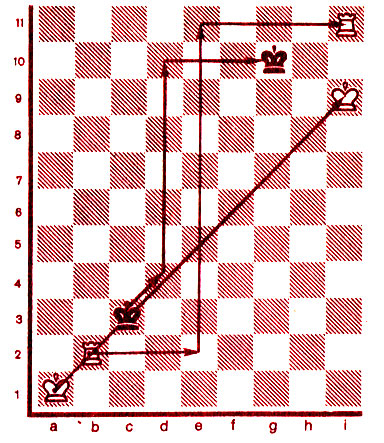
Рис. 87

План матования показан прямо на рисунке 87 в виде траекторий движения всех трех фигур. Нам пришлось добавить к обычной доске одну вертикаль - i и три горизонтали.

1. Ле2! Kpd4. После 1... Kpd3 2. Лe11! у черных будет потерян темп по сравнению с основным вариантом.

2. Kph2 Kpd5 3. Kpc3 Kpd6 4. Kpd4 Kpd7 5. Лe11! Kpd8 6. Kpe5 Kpd9 7. Kpf6 Kpd10. Как будто усилия не увенчались успехом: ладья должна уйти, уступая дорогу черному королю. Однако белые добились важной цели - перебросили своего короля правее ладьи, и теперь обе их фигуры участвуют в окружении.

8. Лe11! Kpe10. Королю остается бежать на восток, но далеко ему не уйти. 9. Kpg7 Kpf10 10. Kph8 Kpg10 11. Kpi9! Все кончено. Черный король отрезан по обоим направлениям и далее матуется как на самой обычной доске.

Любой шахматист, даже начинающий, справится с этой задачей при условии, что он отличается сообразительностью и смекалкой. Компьютеру же остается только позавидовать человеку, способному смотреть на вещи свежим взглядом. На данном примере легко убедиться, что в решении нестандартных задач человек пока еще может дать фору машине! Вы удовлетворены?

- Вполне. И большое спасибо за диалоги.

- И вам спасибо: приятно было побеседовать с интеллигентным молодым человеком. Желаю вам успеха на вступительных экзаменах, а также удачных шахматных баталий.

- Спасибо. А вам разрешите пожелать побыстрее привести в порядок эти диалоги и превратить их в увлекательную книжку.

- Спасибо, как уж получится.

- До свидания.

- До новых встреч!