Глава первая. Учебные окончания

Борьба простых

Оппозиция

Расположение Б. и Ч. шашек на одной вертикали называется оппозицией.

№1. Оппозиция

1. В левой части диаграммы показана ближняя оппозиция, в правой - дальняя. Когда, скажем, Б. делают ход, создающий оппозицию, то говорят - они заняли оппозицию. Ясно, что занявший оппозицию, как ближнюю, так и дальнюю, выигрывает. Если в 1 последний ход сделали, т. е. заняли оппозицию, Ч., то они и выигрывают: 1. 39 19 2. 33 23 ×, или 1. 40 20 2. 34 24 ×.

Оппозиция играет важную роль в борьбе и большего числа пп.

2. Когда борются за оппозицию две пп. против двух, недостатком является разрозненность шашек. Тут более разрознены пп. у Ч. и потому

№2. Разрозненность шашек

а) если ход Ч., то, хотя оппозиция тогда в их пользу, им не выиграть, так как Б. пп. успевают соединиться и, взаимодействуя, прорваться - 1...17 2. 32 22 3. 33 24 4. 32 - 28 (или 4. 33 - 28) =;

б) если же ход Б., то, заняв оппозицию, они заставляют Ч. сдаться - 1. 34 24 2. 31 17 3. 27 ×.

Переставим п. 20 на 19 и оставим ход Ч. Оппозиция сохранилась в их пользу, но выигрыша и теперь нет: Б. успевают сблизить свои пп. и, пожертвовав одну, прорываются другой в дамки - 1...17 2. 32 22 3. 33 23 4. 32 - 28 32 5. 29 с ничьей.

3. Оппозиция в пользу Ч., но опять-таки она еще не обеспечивает им победу - 1...11 2. 27 17 3. 29 19 4. 22 28 5. 23 =.

№3. Оппозиция в пользу Ч

А теперь все шашки сдвиньте по диагонали вправо-вниз (Б. пп. 37, 40; Ч. пп. 11, 20). Снова ход Ч. Здесь оппозиция уже приносит им выигрыш - 1...17 2. 32 22 3. 34 24 4. 29 33 5. 28 27 6. 39 32 7. 33 37 и т. д. ×.

Другой результат после сдвига объясняется тем, что изменилась длина пути пп. до дамочного ряда. Отсюда вывод: владение оппозицией - преимущество, но может ли противник спастись, показывает расчет.

Размен и темп

4. Если Б. пытаются прорваться в дамки, атакуя п. 29, они терпят поражение: 1. 40 10 2 39 - 34 33 3. 30 39 4. 24 14 5. 35 43 6. 30 48 ×; или 1. 40 10 2. 39 - 34 33 3. 35 38 4. 29 42 5. 23 48 6. 18 26 7. 13 14 8. 30 19 и 9...37 ×.

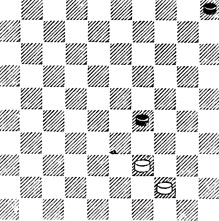
№4. Б. пытаются прорваться в дамки

А если Б. играют на оппозицию? Попробуем: 1. 40 10 2. 35 14 3. 30 19! 4. 25 24 ×.

Результат тот же, так как оппозиция в пользу Ч. Выходит, у Б. спасения нет? Есть! И даже выигрыш! Только играть нужно так: 1. 40 10 2. 35 14 3. 34! 40 4. 44 - Б. занимают оппозицию и выигрывают. Что же столь резко повлияло на итог? Размен! Без него оппозиция складывалась в пользу Ч., а с ним стала выгодной для Б.

Итак, размен передает владение оппозицией другой стороне. Вывод. Когда оппозиция намечается в пользу противника, надо искать размен.

5. Попробуем играть за Б. - 1. 44 14 2. 39 9 3. 33 13 4. 28 18 5. 21 11, и Ч. выиграли, так как завладели оппозицией.

№5. Ч. выиграли

Испытаем другой путь - 1. 44 14 2. 39 9 3. 34 13 4. 30. В этом вар. игра закончится вничью. Удовлетвориться? Нет! Б. должны искать размен: тогда владение оппозицией перейдет к ним и, может быть, принесет выигрыш. Сами Б. осуществить размен не могут... А если заставить разменяться Ч.?

1. 19! с угрозой 2. 13, что вынуждает Ч. либо сразу разменяться путем 1...14, либо ответить 1...9. То, что при 1...14 2. 10 15 3. 45 оппозиция принесет Б. выигрыш,- ясно. Рассмотрим второе продолжение.

1...9 2. 44 15 3. 39 11 4. 21 14 (если 4...20, то 5. 14 и т. д. ×) 5. 10 4 - произошел размен, а с ним и передача ключей от оппозиции в руки Б ! 6. 33 9 7. 29 13 8. 23, и Б. выигрывают.

Существует вид размена, не оказывающий влияния на оппозицию - так называемый скользящий размен.

6. В вар. без размена Б. проиграют из-за оппозиции: 1. 43 23 2. 39 29 ×. А при размене? Посмотрим... 1. 42 22 2. 37 27! 3. 21 - размен обеспечен, но... 3...31 4. 26 27 ×.

№6. Б. проиграют

Оппозиция как была в руках Ч., так у них и осталась, и Б. вновь терпят поражение. Размен ничего не изменил, потому что он был скользящий. Почему же при обычном размене владение оппозицией переходит к другой стороне, а при скользящем нет?

7. Рассмотрим вар. без размена - 1. 42 21 2. 37 27 ×. Ч. выиграли, так как оппозиция сложилась в их пользу. Если убрать пп. 43 и 33 и опять пойти 48 - 42 - 37, то снова оппозицию займут Ч. Ну а что произойдет при размене?

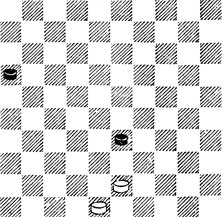
№7. Ч. выиграли

1. 38 42 2. 37 21.

Мы как бы убрали с доски пп. 43 и 33, но Б. сделали два хода подряд 48 - 42 - 37, а Ч. ответили обычным ходом 16- 21. Естественно, что после этого владение оппозицией перешло из одних рук в другие. В подобных случаях говорят, что Б. выиграли темп. Под темпом понимается ход, как единица шашечного времени.

А что получается при скользящем размене? В позиции 6 сделаем ходы - 1. 42 22 2. 37 27 3. 21 31. И размен - 4. 26 27.

Какие изменения произошли? Мы убрали с доски пару стоявших в оппозиции пп. (21 и 31), при этом и Б. и Ч. сделали по двойному ходу, значит, темп никто не выиграл и владение оппозицией сохранилось за прежней стороной.

Приемы борьбы за оппозицию

8. 1. 26! (но не 1. 34? 21! с ничьей) 1...10 2. 34 14. Оппозиция складывается в пользу Ч.? Да. Но у Б. будет размен! 3. 29 19 4. 27 31 5. 37 ×.

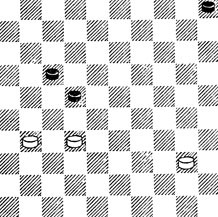
№8. Выигрыш

9. Б. должны немедленно разменяться - 1. 34 40 2. 34 ×. Промедли они с разменом - ничья: 1. 40? 20 2. 35 34! 3. 30 25 4. 24 30 5. 19 34 =.

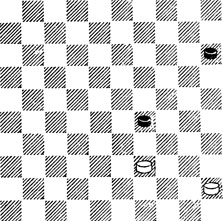
№9. И. Мозер 1941. Выигрыш

Иногда, чтобы занять оппозицию, нужно пожертвовать шашку.

10. 1. 31 22. Ч. п. 22 угрожает проскользнуть в дамки, но - 2. 27! 31 3. 41 - оппозиция! 3...36 4. 37 42 5. 31 - размен оппозицию не меняет: он тут скользящий - 5...27 6. 37 ×.

№10. И. Вейс 1934. Выигрыш

11. 1. 39 18 2. 33 40 (если 2...22, то 3. 28 и 4. 40 ×) 3. 34 22 4. 28! 33 5. 29 и 6. 44 ×.

№11. П. ван Дейк 1938. Выигрыш

12. Тут Ч. сыграли 1...24?, и партия закончилась вничью. А они могли выиграть с помощью оппозиции - 1...40! 2. 45 22 - 28 3. 27 33 4. 28 21 5. 27 24 ×.

№12. Кришта - Янев Суздаль, 1981. Ход черных

13. Не ведет к выигрышу 1. 32?, так как оппозиция при соединенных Ч. пп. не смертельна. Их нужно разобщить. 1. 39! 22 2. 34 23 - 28 3. 29 27 4. 23! и 5. 29 ×.

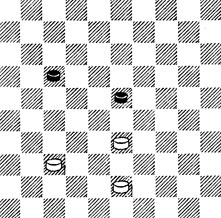
№13. Ж. Бальдан 1881. Выигрыш

14. Тут (из партии) Б. прямолинейно заняли оппозицию - 1. 33? Но после 1...24 - 29 2. 24 28 Ч. пп. соединились и прорвались. К выигрышу вела разобщительная жертва - 1. 30! 35 2. 33 ×.

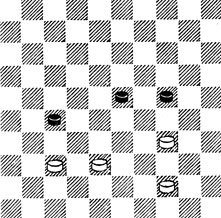
№14. Выигрыш

15. Б. выигрывают, заняв так называемую усиленную оппозицию. 1. 27 31 2. 27 17 (2...16 3. 22 11 4. 18 17 5. 13 и т. д. ×) 3. 27 - 21 22 4. 17! 11 5. 21. Одна Б. п. держит две Ч. 5...16 6. 17 ×.

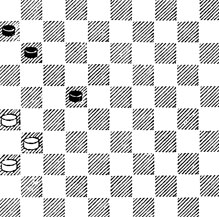
№15. Блонд 1800. Выигрыш

16. Здесь усиленная оппозиция - единственное средство, спасающее Б. от поражения. 1. 44 - 40 39 2. 20! 25 3. 34 30 4. 40 =.

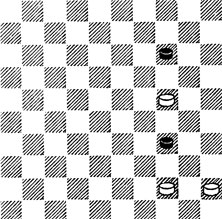
№16. Ю. Барский 1970. Ничья

Отбрасывание

Прием, связанный с жертвой шашки.

17. Обе Б. пп. одинаково далеки от дамочного ряда. Какую двинуть раньше? Может быть, все равно? Нет! 1. 21 - только так! 1...18 2. 24. Прямолинейное 2. 17? вело к ничьей: Ч. п. проскользнула бы в дамки. Теперь же Б. при любом ответе смогут жертвой шашки отбросить Ч. п. назад: если 2...23, то 3. 19 14 4. 17 ×, а если 2...22, то 3. 17 11 4. 19 ×.

№17. Ю. Барский 1970. Выигрыш

А почему не выигрывало 1. 24? Тогда 1...17!, и Б. не смогли бы отбросить Ч. п.

18. 1. 32 31. Если теперь Б. п. 32 бесхитростно устремится в дамки, спастись не удастся: 2. 28? 37 3. 22 42 4. 18 48 и из-за угрозы 5...44 Б. проигрывают. Спасало только отбрасывание - 2. 45! 44 3. 40 35 4. 28 с ничьей: сейчас задержать эту п. невозможно.

№18. Г. Пелле 1928. Ничья

Тактическая тонкость

Под ней понимается неожиданное использование одного из правил взятия (чаще всего "правила большинства") или внезапная меняющая ситуацию жертва шашки.

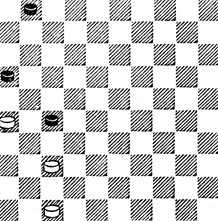
№19. И. Вейс 1916. Выигрыш

19. 1. 41! На первый взгляд странный ход, но только он и приводит к выигрышу. 1...31 2. 32 37 3. 21! Весь план Б. опирается на эту тактическую тонкость. 3...38 4. 43, и оппозиция сложится в пользу Б. Не спасло бы Ч. и 1...7 2. 36 12 3. 37 - 31 17 4. 11 7 5. 21 12 6. 17! и 7. 31 ×.

№20. Ю. Шмидт 1937. Ничья

20. 1. 37 32 2. 21 11 3. 38!! 43 4. 30, и ввиду занятой Б. оппозиции на двух околобортовых вертикалях Ч. не могут ставить Д. ни на 48, ни на 49: в обоих случаях - ничья.

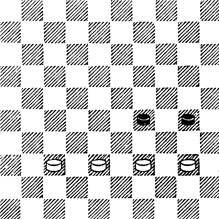
№21. Ж. Феро 1925. Выигрыш

21. Ч. пп. грозят прорваться — как отразить эту угрозу? 1. 38 — 32! 35 2. 33! 27 3. 34 ×.

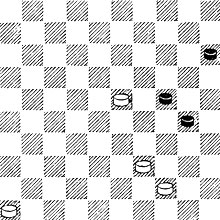
№22. М. Фабр 1933. Выигрыш

22. Опять-таки реализовать перевес Б. помогает тактическая тонкость. 1. 41 20 2. 37 25 3. 32 35 4. 28 24 - 30. Ч. готовы разменяться, однако 5. 19! разрушает их надежды. 5...34 6. 30 13 7. 23 ×.

В следующем примере Б., жертвуя одну п., обеспечивают для второй зеленую улицу к дамочному ряду.

№23. А. Бородин 1984. Ничья

23. На оппозицию рассчитывать не приходится, и борьба сводится к гонке пп. в дамки, в чем Ч. шашки уже имеют большую фору.

1. 37 (1. 42? 32 2 . 36 23! ×; 1. 36? 23 2. 42 32 ×) 1...23 2. 42 29 3. 38 34 4. 37 - 32 31 (но не 4...39? 5. 21 44 6. 33 49 7. 16 =) 5. 33!! (подготовить жертву важнее, чем слепо бросить вперед п. 32) 5...36.

Если 5...40, то 6. 27! 22 7. 29 44 8. 24 49 9. 19 = .

6. 29!

Только жертва спасает Б. Если же 6. 27?, то 6...40 7. 21 (7. 29 44 8. 24 49 9. 22 (а) 41 10. 19 (6) 47 11. 17 (б) 20 12. 11 (г) 40 ×) 7...44 8. 28 50 9. 23 41 10. 18 46 11. 13 (11. 12 23 12. 8 12 ×) 11...22 12. 8 27 ×:

а) 9. 19 21 10. 14 27 11. 10 32 ×.

б) 10. 17 35 11. 20 46 12. 12 2 × или 12. 11 40 ×;

в) 11. 14 32 12 . 9 28 ×; 11. 13 27 12. 31 36 ×;

г) 12. 12 (или 12. 13) 12...35 ×.

6...23 7. 27 41 8. 21 47 9. 17, и Б. п. проходит в дамки! Ничья.