Ним и другие

Во многих играх имеется несколько кучек одинаковых предметов, из которых игроки поочередно берут какое-то число предметов, придерживаясь определенных ограничений, а выигрывает (в некоторых играх, наоборот, проигрывает) игрок, взявший последний предмет. В пределах каждой кучки предметы иногда бывают как-то упорядочены, но различные кучки независимы. Мы называем подобные игры играми типа нима. Они составляют большой класс, так же как, например, шашечные или шахматные игры. Из уже упоминавшихся в этой книге игр к этому классу относятся так-тикс и "щёлк".

Сама игра ним заключается в следующем. Двое игроков по очереди берут предметы из имеющихся нескольких кучек, при этом разрешается брать любое ненулевое их количество, но лишь из какой-то одной кучки. Выигрывает тот, кто берет последний предмет.

Этимология названия "ним" неясна. Впервые его ввел профессор Гарвардского университета Ч.-Л. Бутон, но чем он при этом руководствовался - неизвестно. В английском языке слово nim когда-то означало "брать", а сейчас является жаргонным и означает "стянуть". Имеет ли это какое-нибудь отношение к происхождению названия игры? Вполне возможно.

Теория игр типа нима хорошо разработана. Про сам ним известно всё, так что мы могли бы поместить этот материал в первый раздел книги. Мы не сделали этого потому, что есть другие игры типа нима, для которых законченной теории пока не создано.

Чтобы рассказать о ниме и некоторых других играх, нам придется сделать небольшое математическое отступление.

Читатель привык записывать числа при помощи арабских цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Задумывался ли он когда-нибудь о том, почему этих цифр именно десять? Или что было бы, если бы цифр было какое-то другое количество? Скорее всего, нет, если только читатель - не математик. Мы так привыкли считать десятками, что даже не задумываемся над другими возможностями. А между тем считать предметы можно не десятками, а, скажем, двойками, тройками или дюжинами, и если бы у нас было не десять пальцев на руках, мы бы, наверно, использовали для записи чисел не десять цифр, а какое-нибудь другое их количество. Здесь нам понадобится освоить счет двойками (математики говорят - двоичную систему счисления). Для такого счета нужны только две цифры - 0 и 1. Забудьте на время, что такое арабские цифры. Есть только 0 и 1. Как при их помощи записывать числа?

Нуль так и записывается - 0, один тоже так и обозначается - 1. Это ясно. А вот число два будет выглядеть так: 10. Это не десять, а два - ведь мы договорились, что цифр 2, 3, 4, 5, 6, 7, 8, 9 в нашем распоряжении нет! Следующее число - три - записывается двумя единицами - 11. Затем следует 100 - это четыре, затем 101 - это пять и т. д. Числа в такой записи называют двоичными, в отличие от десятичных чисел, записываемых обычным образом. Вам потребуется (если вы хотите научиться безошибочно играть в ним) освоить двоичную запись чисел так, чтобы уметь быстро записывать любое число при помощи только 0 и 1. Вот как это можно делать. Пусть есть число. Поделите его на два и запишите остаток от деления - им будет 0 или 1. Затем результат деления снова поделите на два и остаток припишите слева. Так продолжайте до тех пор, пока в результате деления не получите единицу. Тогда не делите ее, а просто припишите слева. Полученная запись и есть двоичная запись вашего числа.

Например, запишем 10 в двоичной форме. Делим на два, имеем 5 и остаток нуль. Пишем 0. Теперь 5 делим на два, имеем 2 и остаток один. Приписываем слева 1. Теперь 2 делим на два, получаем 1 и остаток нуль. Приписываем слева 0. Единицу делить на два, как уже было сказано, не надо. Просто дописываем ее слева. Окончательно получается: 1010. Это и есть двоичная запись числа 10. Как видите, записывать числа в двоичной форме совсем просто.

Как же всё-таки правильно играть в ним? Для объяснения этого нам понадобится ввести понятие так называемой ним-суммы. Пусть количество предметов в первой кучке равно N₁, во второй N₂, в третьей N₃ и т. д. Набор чисел N₁, N₂, N₃, ... полностью определяет положение на доске (игровую позицию). Запишем числа N₁, N₂, N₃, ... в двоичной форме друг под другом и сложим столбиком (как обычные, а не двоичные числа), после чего каждую цифру в сумме заменим остатком от деления ее на два, т. е. на 0, если она четная, и на 1, если она нечетная. Получится некое двоичное число. Оно и называется ним-суммой чисел N₁, N₂, N₃, ... Например, пусть в первой кучке 3 предмета, во второй - 4, в третьей - 5. Вычислим ним-сумму для этой позиции:

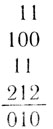
Как видите, она равна двойке (двоичное число 10, как вы помните, есть двойка).

А теперь само правило, следуя которому вы будете играть безошибочно. Вот оно: надо каждый раз делать такой ход, чтобы ним-сумма для получающейся позиции была равна нулю. Позиции, для которых ним-сумма равна нулю, называют безопасными, а остальные позиции опасными, так что правило можно переформулировать так: каждым ходом надо создавать безопасную позицию.

Если позиция безопасна, то всякий ход переводит ее в опасную - это первое свойство ним-суммы, которое лежит в основе стратегии игры в ним. Второе свойство таково: если позиция опасна, всегда существует ход, переводящий ее в безопасную. Из этих свойств следует, что если ваша очередь делать ход в позиции, которая опасна, то вы можете добиться победы, следуя вышеприведенному правилу. В самом деле, вы переводите позицию в безопасную (это можно сделать согласно второму свойству ним-суммы), противник вынужден (согласно первому свойству ним-суммы) перевести ее в опасную, а вы снова делаете ее безопасной и т. д. Но общее количество предметов в кучках всё время уменьшается, и в конце концов наступает момент, когда кто-то берет последний предмет. Кто его берет? Его не может взять противник, потому что тогда получилось бы, что он сделал позицию безопасной (ведь позиция, в которой все кучки пусты, как легко видеть, безопасна - ним-сумма равна нулю), а мы знаем, что все ходы противника могут приводить лишь к опасным позициям, поскольку все они совершаются в безопасных позициях. Следовательно, последний предмет берете вы.

Если вам выпало делать первый ход в позиции, которая уже безопасна, то вся ваша надежда на то, что противник не знает правила. Если он его знает, ваше положение безнадежно.

На первый взгляд, во всем этом есть какая-то мистика. Ведь всемогущее правило взялось непонятно откуда. На самом деле это не так, но объяснять, откуда же взялось правило, мы здесь не будем - всё-таки эта книга написана не для математиков.

Чтобы читатель окончательно уверовал в правило, приведем пример партии в ним.

Пример партии

Пусть начальная позиция такова: в первой кучке 3 предмета, во второй - 4, в третьей - 5. Мы уже считали для нее ним-сумму. Она оказалась равна двойке. Итак, позиция опасна. Следовательно, тот, кто начинает, выигрывает. Вот как это происходит.

Первый игрок берет два предмета из первой кучки, получая позицию (1, 4, 5). Ее ним-сумма, как читатель может сосчитать, нулевая. Второй игрок берет, скажем, два предмета из третьей кучки, получая (1, 4, 3). В ответ первый игрок берет два предмета из второй кучки. Возникшая позиция (1, 2, 3) снова безопасна. Второй игрок забирает предмет из первой кучки (0, 2, 3). Тогда первый забирает один предмет из третьей кучки (0, 2, 2). Финал ясен. Второй игрок переводит позицию в (0, 1, 2), первый - в (0, 1, 1), второй - в (0, 0, 1), и первый забирает последний предмет и выигрывает.

Как уже говорилось, существует множество игр типа нима. Например, в китайской народной игре цзяньшицзы (любопытно, что ее предложил также В. Витхофф в качестве усложнения нима, не зная, что в Китае в нее играют с давних пор) имеются две кучки предметов, причем разрешается брать либо произвольное количество предметов из одной кучки, либо сразу из двух кучек, но непременно поровну. Выигрывает тот, кто берет последний предмет. Теория этой игры относительно сложна, и мы не будем ее приводить.

В игре "кегли" предметы в каждой кучке выложены в ряд. Разрешается брать из любой кучки либо один предмет, либо два соседних предмета. Если взятие происходит из середины ряда, он тем самым разбивается на два, так что число кучек может возрастать. Выигравшим считается взявший последний предмет. Теория этой игры также не так проста, чтобы можно было здесь о ней рассказывать.

Тривиальна игра Баше, в которой двое игроков берут поочередно предметы в любом количестве, не превосходящем некоторого заданного числа, из единственной кучки, а выигрывает взявший последний предмет. Если N - число предметов в кучке, а М - число, ограничивающее взятие, то, очевидно, первый игрок всегда может выиграть, кроме случая, когда N делится на М + 1. Для этого он должен всякий раз брать столько предметов, чтобы количество оставшихся предметов делилось на М + 1. Именно эти позиции в данной игре являются безопасными, причем, как и в случае нима, опасную позицию всегда можно превратить в безопасную, а из безопасной может получиться только опасная.

Если в игре Баше вместо одной кучки предметов использовать несколько, получится такое ее обобщение, которое является одновременно модификацией нима. В этом случае безопасными будут те позиции, для которых ним-сумма остатков от деления на M + 1 количеств предметов в кучках равна нулю, а правило снова состоит в том, чтобы получать безопасные позиции.

В игре Мура разрешается брать предметы в произвольном количестве из нескольких кучек сразу, но не больше, чем из заданного числа (обозначим это число через М). Эта игра своей стратегией почти не отличается от нима, надо только при вычислении ним-суммы заменять цифры суммы N₁ + N₂ + N₃ + ... (числа N₁, N₂, N₃, ... записываются, как и прежде, друг под другом в двоичной форме и складываются столбиком) не остатками от деления на два, а остатками от деления на М + 1. Безопасными будут позиции с нулевой ним-суммой. Очевидно, ним является частным случаем игры Мура, в котором М = 1.

О многих других модификациях нима читатель может узнать из довольно обширной, но, увы, чаще всего специальной литературы. Из доступных большинству читателей книг можно порекомендовать "Крестики-нолики" М. Гарднера, где рассказывается, в частности, о придуманной Дж. Конуэем замечательной игре "Усадьба Хакенбуш".

Все игры типа нима обратимы. Иногда обращение может быть тривиальным. Например, обратный "щёлк", где выигрывает взявший последнюю фишку, совершенно неинтересен, так как партия в него длится ровно один ход - своим первым ходом первый игрок забирает все фишки. Однако случается и так, что обращение повышает сложность игры.

Сам ним - пример игры, обращение которой по своей стратегии ничуть не отличается от прямой игры. В обратном ниме игрок, взявший последний предмет, считается не выигравшим, а проигравшим. Оказывается, что в него можно безошибочно играть, придерживаясь обычного правила! Надо только к концу игры оставить нечетное число кучек, в которых будет по одной фишке.